

This article is automatically translated.
Japanese phoneme alignment is a task that assigns which phonemes in a written Japanese sentence are spoken at what intervals in the audio data. This is used in creating machine learning datasets for voice conversion and speech synthesis. Manual phoneme alignment requires a lot of effort, and automatic Japanese phoneme alignment methods sometimes produce results that seem counterintuitive compared to human assignments. To address this, we developed the tool pydomino (https://github.com/DwangoMediaVillage/pydomino), which performs more human-like Japanese phoneme alignment by considering distinctive features. pydomino is open source and can be installed via pip from the following GitHub repository and used immediately without requiring a GPU.
git clone --recursive https://github.com/DwangoMediaVillage/pydomino
cd pydomino
pip install .
This page introduces the phoneme alignment method that considers distinctive features, which is the core algorithm of pydomino, and the comparative experiments using the ITA corpus multimodal database.
Phoneme alignment labels which phonemes are being spoken at what times in a given audio. The sequence of phonemes is provided initially. There are no times when multiple labels are assigned simultaneously, and no times without any labels.

These labels are 39 phonemes shown in Table 1. Here, they are generally associated with sounds similarly to Hepburn romanization. For example, “i” is the vowel “い”, “u” is the vowel “う”, “k” is a consonant in the k-row, and “n” is a consonant in the n-row. Labels not found in Hepburn romanization, such as “pau”, “N”, “I”, “U”, and “cl” represent “pause”, nasal “ん”, devoiced “i”, devoiced “u”, and geminate consonant “っ” respectively.
| pau | ry | r | my | m | ny |
| n | j | z | by | b | dy |
| k | ch | ts | sh | s | hy |
| h | v | d | gy | g | ky |
| f | py | p | t | y | w |
| N | a | i | u | e | o |
| I | U | cl |
Therefore, phoneme alignment is framed as predicting the time intervals for each phoneme from the speech waveform data and the read phoneme data.
| Input | 16kHz single-channel audio waveform | \( \boldsymbol{x} \in [0, 1]^{T} \) |
| Sequence of read phonemes | \( \boldsymbol{l} \in \Omega^{M} \) | |
| Output | Time intervals for each phoneme | \( \boldsymbol{Z} \in \mathbb{R}_{+}^{M \times 2} \) |
Here, the sequence of read phonemes \( \boldsymbol{l} = (l_1, l_2, \cdots l_M) \) has “pau” phonemes at both ends (\( l_1 = l_M = \mathrm{pau} \)), and the time intervals \(\boldsymbol{Z} = [\boldsymbol{z}_1, \boldsymbol{z}_2, \cdots \boldsymbol{z}_M]^{\top}\) are represented as \(\boldsymbol{z}_m = [z_{m1}, z_{m2}]\), indicating that phoneme \( l_m \) is spoken between \( z_{m1} \) and \( z_{m2} \) seconds.
Solving this problem allows the use of time intervals for each phoneme in tasks such as voice conversion (Voice Conversion) and text-to-speech (Text-to-Speech) model training. For example, Seiren Voice improves voice conversion quality using phoneme alignment [1]. Generally, preparing the time intervals for each phoneme requires manual labeling. However, this labeling process is skill-intensive and time-consuming. Thus, it is expected that machine learning can replace manual labeling, but machine learning results can sometimes seem counterintuitive when compared by human listeners.
Recent studies have proposed text-to-speech systems that can self-supervise and acquire time interval information without manually prepared labels during training. However, this self-acquired interval information does not always match actual audio data, making it difficult to control the timing of pronunciations when corrections are needed later.
Therefore, pydomino aims to automatically estimate interval information close to human-created label data. Focusing on distinctive features designed based on phonetics, we improved phoneme alignment performance.
Phoneme alignment generally calculates an alignment weight matrix \( \boldsymbol{A} \in \mathbb{R}^{T' \times M} \), which is used in Dynamic Time Wrapping (DTW) [2] to estimate which phoneme is being read at each time frame. Here, \( T' \) is the number of time frames in the input audio data, and \( M \) is the total number of phonemes in the read text.
There are several methods to calculate this alignment weight matrix \( \boldsymbol{A} \), such as solving a classification task for each time frame using hard-aligned label data as supervision [3] [5] or using CTC Loss with non-aligned phoneme read data [4] [5] [6]. Another approach integrates attention weights into the model for speech separation tasks without directly expressing the loss [7].
Phonemes have similarities and dissimilarities when heard. For example, “ry” (consonant in the “りゃ” row) is similar to “r” (consonant in the “ら” row), but “ry” (consonant in the “りゃ” row) is less similar to “w” (consonant in the “わ” row). Such well-known phoneme similarities are not explicitly considered in methods using classification loss, CTC loss, or attention-based approaches. Therefore, we designed phoneme features based on distinctive features, as shown in the table below. + indicates positive, - indicates negative, and blank means undefined.
| 音素 | 両唇音 | 歯茎音 | 硬口蓋音 | 軟口蓋音 | 口蓋垂音 | 声門音 | 破裂音 | 鼻音 | はじき音 | 摩擦音 | 接近音 | 円唇音 | 非円唇音 | 前舌音 | 後舌音 | 広母音 | 半狭母音 | 狭母音 | 子音性 | 共鳴音 | 接近性 | 音節性 | 有声性 | 継続性 | 促音 | 無音 |
| ry | - | + | + | - | - | - | - | - | + | - | - | + | + | + | - | + | - | |||||||||
| r | - | + | - | - | - | - | - | - | + | - | - | + | + | + | - | + | - | |||||||||
| my | + | - | + | - | - | - | - | + | - | - | - | + | + | - | - | + | - | |||||||||
| m | + | - | - | - | - | - | - | + | - | - | - | + | + | - | - | + | - | |||||||||
| ny | - | - | + | - | - | - | - | + | - | - | - | + | + | - | - | + | - | |||||||||
| n | - | + | - | - | - | - | - | + | - | - | - | + | + | - | - | + | - | |||||||||
| j | - | + | + | - | - | - | + | - | - | + | - | + | - | - | - | + | - | |||||||||
| z | - | + | - | - | - | - | + | - | - | + | - | + | - | - | - | + | - | |||||||||
| by | + | - | + | - | - | - | + | - | - | - | - | + | - | - | - | + | - | |||||||||
| b | + | - | - | - | - | - | + | - | - | - | - | + | - | - | - | + | - | |||||||||
| dy | - | + | + | - | - | - | + | - | - | - | - | + | - | - | - | + | - | |||||||||
| d | - | + | - | - | - | - | + | - | - | - | - | + | - | - | - | + | - | |||||||||
| gy | - | - | + | + | - | - | + | - | - | - | - | + | - | - | - | + | - | |||||||||
| g | - | - | - | + | - | - | + | - | - | - | - | + | - | - | - | + | - | |||||||||
| ky | - | - | + | + | - | - | + | - | - | - | - | + | - | - | - | - | - | |||||||||
| k | - | - | - | + | - | - | + | - | - | - | - | + | - | - | - | - | - | |||||||||
| ch | - | + | + | - | - | - | + | - | - | + | - | + | - | - | - | - | - | |||||||||
| ts | - | + | - | - | - | - | + | - | - | + | - | + | - | - | - | - | - | |||||||||
| sh | - | + | + | - | - | - | - | - | - | + | - | + | - | - | - | - | + | |||||||||
| s | - | + | - | - | - | - | - | - | - | + | - | + | - | - | - | - | + | |||||||||
| hy | - | - | + | - | - | + | - | - | - | + | - | + | - | - | - | - | + | |||||||||
| h | - | - | - | - | - | + | - | - | - | + | - | + | - | - | - | - | + | |||||||||
| v | + | - | - | - | - | - | - | - | - | + | - | + | - | - | - | + | + | |||||||||
| f | + | - | - | - | - | - | - | - | - | + | - | + | - | - | - | - | + | |||||||||
| py | + | - | + | - | - | - | + | - | - | - | - | + | - | - | - | - | - | |||||||||
| p | + | - | - | - | - | - | + | - | - | - | - | + | - | - | - | - | - | |||||||||
| t | - | + | - | - | - | - | + | - | - | - | - | + | - | - | - | - | - | |||||||||
| y | - | - | + | - | - | - | - | - | - | - | + | - | + | + | - | + | + | |||||||||
| w | + | - | - | - | - | - | - | - | - | - | + | - | + | + | - | + | + | |||||||||
| N | - | - | - | - | + | - | - | + | - | - | - | + | + | - | - | + | - | |||||||||
| a | - | + | + | - | + | - | - | - | + | + | + | + | + | |||||||||||||
| i | - | + | + | - | - | - | + | - | + | + | + | + | + | |||||||||||||
| u | - | + | - | + | - | - | + | - | + | + | + | + | + | |||||||||||||
| e | - | + | + | - | - | + | - | - | + | + | + | + | + | |||||||||||||
| o | + | - | - | + | - | + | - | - | + | + | + | + | + | |||||||||||||
| I | - | + | + | - | - | - | + | - | + | + | + | - | - | |||||||||||||
| U | - | + | - | + | - | - | + | - | + | + | + | - | - | |||||||||||||
| cl | - | - | + | |||||||||||||||||||||||
| pau | - | - | + |
By explicitly utilizing these features, it becomes possible to learn alignment while considering the similarities between phonemes.
During training and inference, consonants associated with the vowel phonemes “i” and “I” are rewritten to consonants with palatalized versions of those consonants. For example, “ki (k i)” is converted to “ky i”. This is because the pronunciation of the “i” row in Japanese is palatalized, making it closer to the actual pronunciation of palatalized sounds. Therefore, “ki” belongs to the “kya, kyi, kyu, kye, kyo” group rather than the “ka, ki, ku, ke, ko” group.
For input audio of 16kHz mono sound source, after performing short-time Fourier transform with a window width of 400 and a hop width of 160 using a Hann window, it is converted to an 80-dimensional logarithmic mel spectrogram as input features for the neural network. This means each time frame of input corresponds to 10 milliseconds, and therefore the alignment is also predicted in 10-millisecond units.
The loss during training, \(\mathcal{L}\), is calculated as the binary cross entropy for each phoneme feature.
$$ \mathcal{L} = \sum_{t=1}^{T'}\sum_{i \in I} y_{ti} \log \pi_{ti} + (1 - y_{ti}) \log (1 - \pi_{ti}) $$Here, \(T'\) is the number of time frames, \(I\) is the set of previously mentioned phoneme features, \(y_{ti}\) is a binary variable label indicating whether feature \(i\) is positive at time \(t\), and \(\pi_{ti}\) is the probability that feature \(i\) is positive at time \(t\), which is the output of the neural network.
For alignment of each time frame, this method uses the Viterbi algorithm [8]. When aligning, the minimum allocation time per phoneme is set to consider the length of phonemes.
Before applying the Viterbi algorithm, the posterior probability of phonemes \(p_{tv}\) at time \(t\) is calculated based on the predicted probabilities of features \(\boldsymbol{\Pi} \in [0, 1]^{T' \times |\Omega| }\) obtained by the neural network. The posterior probability of phoneme \(v \in \Omega\) at time \(t\) is given by
$$ p_{tv} = \frac{ \prod_{i} \pi_{ti}^{y_{vi}} (1 - \pi_{ti})^{(1 - {y_{vi}})}}{\sum_{v \in \Omega} \prod_{i} \pi_{ti}^{y_{vi}} (1 - \pi_{ti})^{(1 - {y_{vi}})}} $$To prevent numerical underflow, the actual calculation is done in the logarithmic domain.
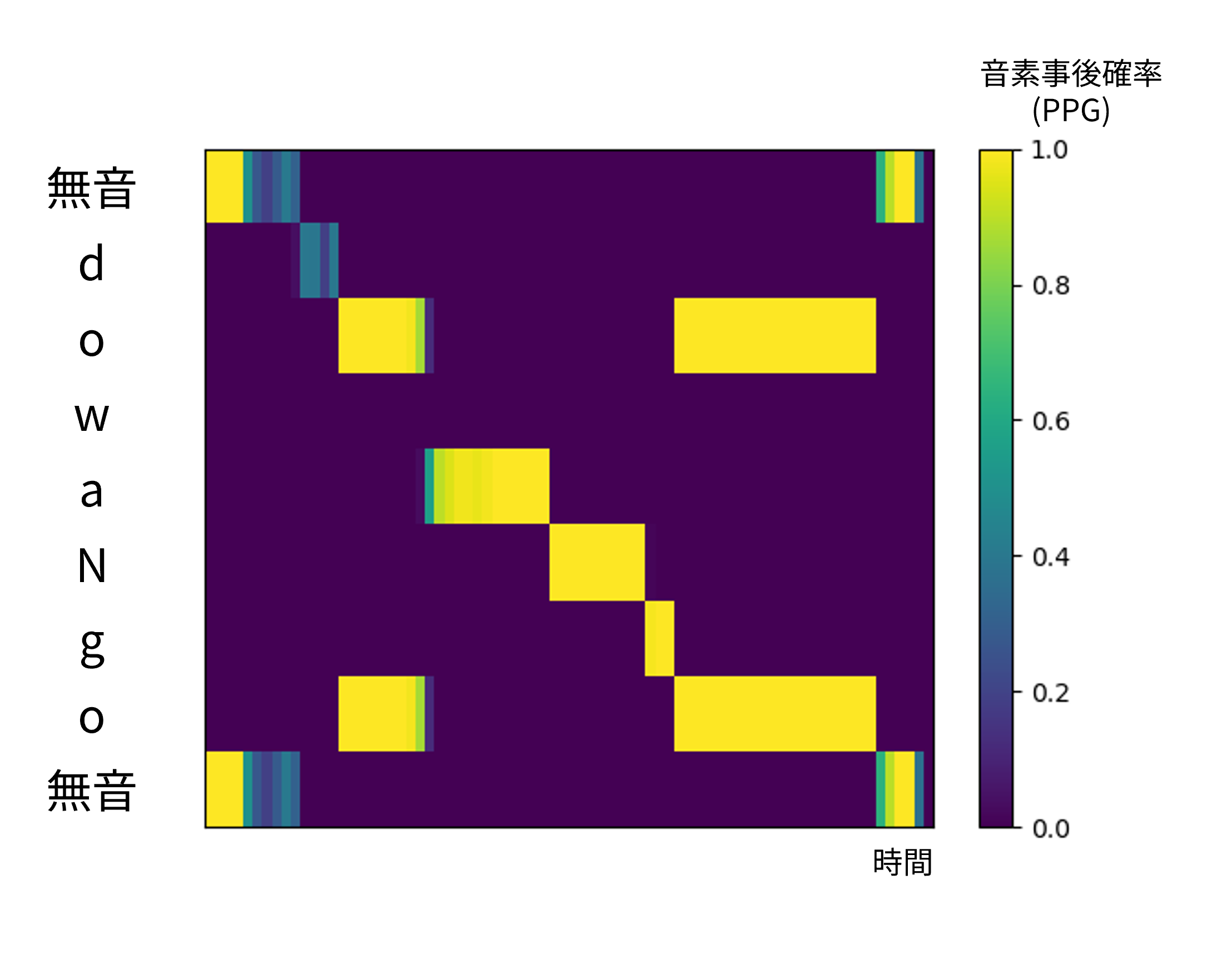
A common mistake with DTW alignment is that some phonemes read out at the prediction stage of the network cannot be predicted, and the Viterbi algorithm assigns only one time frame to them. For example, in Figure 2, it can be seen that the alignment weight for “w” is not assigned. In this case, the Viterbi algorithm infers to minimize the time assigned to “w”. However, since it is guaranteed that the input phonemes are read in the audio data in the problem setting of this paper, we introduced a minimum allocation time frame to ensure the pronunciation of phonemes that the network could not predict.
The pseudocode is as follows. \(N = 1\) is equivalent to the general Viterbi algorithm.
\begin{algorithm}
\caption{Viterbi Algorithm}
\begin{algorithmic}
\INPUT $\boldsymbol{P} \in \mathbb{R}^{T' \times |\Omega|},$ $\boldsymbol{l} \in \Omega^{M},$ $N \in \mathbb{Z}_{+}$
\OUTPUT $\boldsymbol{Z} \in \mathbb{R}_{\ge 0}^{M \times 2}$
\STATE $\boldsymbol{A} \in \mathbb{R}^{T' \times M} =$\CALL{initialize}{$\boldsymbol{P}, \boldsymbol{l}$}
\STATE $\boldsymbol{\beta} \in \mathbb{B}^{T' \times M} =$\CALL{forward}{$\boldsymbol{A}, T', N$}
\STATE $\boldsymbol{Z} \in \mathbb{R}_{\ge 0}^{M \times 2} =$\CALL{backtrace}{$\boldsymbol{\beta}, T', N$}
\end{algorithmic}
\end{algorithm}
\begin{algorithm}
\caption{Initialize}
\begin{algorithmic}
\INPUT $\boldsymbol{P} \in \mathbb{R}^{T' \times |\Omega|}, \boldsymbol{l} \in \Omega^{M}$
\OUTPUT $\boldsymbol{A} \in \mathbb{R}^{T' \times M}$
\FOR{$t = 1$ \TO $T'$}
\FOR{$m = 1$ \TO $M$}
\STATE $a_{tm} = p_{t,l_m}$
\ENDFOR
\ENDFOR
\end{algorithmic}
\end{algorithm}
\begin{algorithm}
\caption{Backtracing}
\begin{algorithmic}
\INPUT $\boldsymbol{\beta} \in \mathbb{B}^{T' \times M}, N \in \mathbb{Z}_{+}$
\OUTPUT $\boldsymbol{Z} \in \mathbb{R}_{\ge 0}^{M \times 2}$
\STATE $t=T'$
\STATE $m=M$
\STATE $z_{m1} = T' / 100$
\WHILE{$t > 0$}
\IF{$\beta_{tm}$}
\STATE ${t = t - N}$
\STATE $z_{m0}$ $= (t+1) / 100$
\STATE ${m = m - 1}$
\STATE $z_{m1} = t / 100$
\ELSE
\STATE $t = t - 1$
\ENDIF
\ENDWHILE
\STATE $z_{00} = 0.0$
\end{algorithmic}
\end{algorithm}
\begin{algorithm}
\caption{Forwarding}
\begin{algorithmic}
\INPUT $\boldsymbol{A} \in \mathbb{R}^{T' \times M}, N \in \mathbb{Z}_{+}$
\OUTPUT $\boldsymbol{\beta} \in \mathbb{B}^{T' \times M}$
\FOR{$t = 1$ \TO $T'$}
\FOR{$m = 1$ \TO $M$}
\IF{$t = 1$ \AND $m=1$}
\STATE $\alpha_{tm} = a_{tm}$
\ELSE
\STATE $\alpha_{tm} = -\infty$
\ENDIF
\ENDFOR
\ENDFOR
\FOR{$t = 1$ \TO $T'$}
\FOR{$m = 1$ \TO $M$}
\STATE $\beta_{tm} =$ \FALSE
\ENDFOR
\ENDFOR
\FOR{$t = N$ \TO $T'$}
\FOR{$m = 2$ \TO $M$}
\STATE $b^{\mathrm{(next)}} = \alpha_{t-N,m-1}$
\FOR{$n=0$ \TO $N-1$}
\STATE $b^{\mathrm{(next)}}$ $= b^{\mathrm{(next)}} + p_{t-n,m}$
\ENDFOR
\STATE $b^{\mathrm{(keep)}} = \alpha_{t-N,m}$
\FOR{$n=0$ \TO $N-1$}
\STATE $b^{\mathrm{(keep)}} = p_{t-n,m}$
\ENDFOR
\IF {$b^{\mathrm{(next)}} > b^{\mathrm{(keep)}}$}
\STATE $\alpha_{tm} = b^{\mathrm{(next)}}$
\STATE $\beta_{tm} = $ \TRUE
\ELSE
\STATE $\alpha_{tm} = b^{\mathrm{(keep)}}$
\ENDIF
\ENDFOR
\ENDFOR
\end{algorithmic}
\end{algorithm}
To verify the effectiveness of the created phoneme features, we conducted comparative experiments with one-hot labels.
The network used in the comparative experiments consisted of 1 MLP layer + 4 bidirectional LSTM layers + 1 MLP layer + Sigmoid function, using ReLU as the activation function. Each layer had 256 hidden units. This network took the logarithmic mel spectrogram created by the method described above as input and output the logits of distinctive features. Detailed input and output settings are described in the next section. We used the Adam optimizer with a learning rate of 1e-3 and no scheduling.
For training, we used the CSJ dataset [9]. The audio in the dataset was segmented to be within 15 seconds using blank intervals for training. The distinctive feature labels were created from the CSJ dataset labels using the Julius segmentation kit [10], converted to a roughness of 10 milliseconds. Rounding was done to the nearest millisecond. For performance evaluation, we used the reading audio and its alignment from the ITA corpus multimodal database [11] for three characters: Zundamon, Tohoku Itako, and Shikoku Metan. The correct labels in the ITA corpus multimodal database are manually created, so we used them for performance evaluation in this paper.
To measure how well pydomino performs as a phoneme alignment tool, we introduced alignment error rate. When dealing with continuous time,
$$ \text{Alignment Error Rate (\%)} = \frac{\text{Duration of mismatched intervals}}{\text{Total duration of audio data}} \times 100 $$can be calculated.
In the experiments, this alignment error rate is calculated for both the alignment data after the Viterbi algorithm output.
To compare with existing Japanese phoneme alignment tools, we aligned the ITA corpus multimodal data using the Julius segmentation kit and compared the results. The models used in the experiment were four combinations: (one-hot vector labels, phoneme feature binary labels) × (with palatalization label rewriting, without palatalization label rewriting). By comparing these four combinations, we verified the effectiveness of the phoneme feature labels and palatalization label rewriting. The results are as follows. The minimum allocation duration per phoneme was set to 50 milliseconds based on the subsequent experiments.
| Alignment Error Rate (%) | |
|---|---|
| 1hot vector / No Palatalization | 14.650 ± 0.324 |
| 1hot vector / With Palatalization | 14.647 ± 0.897 |
| Distinctive Features / No Palatalization | 14.186 ± 0.257 |
| Distinctive Features / With Palatalization (Ours) | 14.080 ± 0.493 |
| Julius Segmentation Kit | 19.258 |
From Table 3, it can be seen that phoneme feature labels are better than one-hot vector labels, and palatalization label rewriting is better than without rewriting in terms of phoneme alignment error rate for the ITA corpus multimodal data. Also, the proposed method has a lower phoneme alignment error rate than the Julius segmentation kit.
The phoneme alignment label data of the ITA corpus multimodal data is manually labeled, indicating that the proposed method can achieve labeling closer to human labeling compared to the Julius segmentation kit.
The reason why the proposed method, even though trained with labels created by the Julius segmentation kit, achieves a phoneme alignment method closer to human perception than the Julius segmentation kit is currently unclear. However, as pointed out in Deep Image Prior [12], it is speculated that the structure of the neural network itself has the same effect as the prior distribution of alignment created by human hands.
The change in alignment error rate when varying the minimum allocation time frame for each phoneme is shown in the figure. The minimum allocation duration is set to 10, 20, 30, 40, 50, 60, 70 milliseconds, corresponding to Algorithm 1~4 with \(N=1, 2, 3, 4, 5, 6, 7\) respectively.
As can be seen from Figure 3, the inference results of the phoneme alignment network trained with distinctive features and palatalized labels are closest to human phoneme alignment data. Furthermore, the phoneme alignment data with a minimum allocation of 50 milliseconds per phoneme is closest to human phoneme alignment data. The error rates of phoneme alignment data with a minimum allocation of 50 milliseconds per phoneme for each model correspond to the average phoneme error rates in Table 3.
In this paper, we introduced a phoneme alignment tool based on the learning of distinctive features and detailed its technical aspects. We predicted distinctive features on a time frame basis, calculated posterior probabilities based on them, and used the Viterbi algorithm for alignment. This enabled us to infer phoneme alignment data closer to human results than the Julius segmentation kit. Furthermore, by introducing a minimum allocation time frame per phoneme in the Viterbi algorithm, we realized a tool that can infer phoneme alignment data closer to human results. Future challenges include further improving phoneme alignment accuracy by refining network structures and distinctive features to be predicted, and developing a phoneme alignment tool that does not require inputting read text by simultaneously inferring the read text.
[1] 変換と高精細化の2段階に分けた声質変換 (2024年4月18日に取得) https://dmv.nico/ja/casestudy/2stack_voice_conversion/
[2] H. Sakoe and S. Chiba, Dynamic programming algorithm optimization for spoken word recognition, IEEE Transactions on Acoustics, Speech, and Signal Processing, vol. 26, no. 1, pp. 43-49, February 1978 https://ieeexplore.ieee.org/document/1163055
[3] Matthew C. Kelley and Benjamin V. Tucker, A Comparison of Input Types to a Deep Neural Network-based Forced Aligner, Interspeech 2018 https://www.isca-archive.org/interspeech_2018/kelley18_interspeech.html
[4] Kevin J. Shih and Rafael Valle and Rohan Badlani and Adrian Lancucki and Wei Ping and Bryan Catanzaro, {RAD}-{TTS}: Parallel Flow-Based {TTS} with Robust Alignment Learning and Diverse Synthesis, ICML Workshop on Invertible Neural Networks, Normalizing Flows, and Explicit Likelihood Models 2021 https://openreview.net/forum?id=0NQwnnwAORi
[5] Jian Zhu and Cong Zhang and David Jurgens, Phone-to-audio alignment without text: A Semi-supervised Approach, ICASSP 2022 https://arxiv.org/abs/2110.03876
[6] Yann Teytaut and Axel Roebel, Phoneme-to-Audio Alignment with Recurrent Neural Networks for Speaking and Singing Voice, Interspeech 2021 https://www.isca-archive.org/interspeech_2021/teytaut21_interspeech.html
[7] K. Schulze-Forster, C. S. J. Doire, G. Richard and R. Badeau, Joint Phoneme Alignment and Text-Informed Speech Separation on Highly Corrupted Speech, ICASSP 2020 https://ieeexplore.ieee.org/abstract/document/9053182
[8] A. Viterbi, Error bounds for convolutional codes and an asymptotically optimum decoding algorithm in IEEE Transactions on Information Theory, vol. 13, no. 2, pp. 260-269, April 1967 https://ieeexplore.ieee.org/document/1054010
[9] Maekawa Kikuo, Corpus of Spontaneous Japanese : its design and evaluation, Proceedings of The ISCA & IEEE Workshop on Spontaneous Speech Processing and Recognition (SSPR 2003) https://www2.ninjal.ac.jp/kikuo/SSPR03.pdf
[10] Julius 音素セグメンテーションキット (2024年4月23日に取得) https://github.com/julius-speech/segmentation-kit
[111] ITAコーパスマルチモーダルデータベース https://zunko.jp/multimodal_dev/login.php
[12] Ulyanov, Dmitry and Vedaldi, Andrea and Lempitsky, Victor, Deep Image Prior, 2020 https://arxiv.org/abs/1711.10925
To investigate which phonemes the palatalization label rewriting is particularly effective for, we compared the alignment error rates for phonemes that underwent palatalization. In this experiment, we used phoneme alignment with a minimum allocation of 50 milliseconds in the Viterbi algorithm for comparison.
For comparing alignment accuracy of the original phoneme and its rewritten version (e.g., for the k-row, “k” and “ky”):
The results show that the alignment error rates for “ny”, “my”, “ry”, “gy”, “dy”, “by” improved with label rewriting, indicating that applying phoneme alignment to consonants with low occurrence frequency in training data is closer to human labeling.
| Consonant | Label Rewriting | Error Rate of Original Consonant (%) | Error Rate of Rewritten Consonant (%) | Error Rate of “i” Row Consonant (%) | Error Rate of Non-“i” Row Original Consonant (%) | Error Rate of Non-“i” Row Rewritten Consonant (%) |
|---|---|---|---|---|---|---|
| k and ky | Yes | 28.114 | 28.153 | 26.170 | 27.080 | 25.638 |
| No | 28.114 | 28.471 | 26.936 | 27.080 | 26.388 | |
| s and sh | Yes | 14.457 | 15.296 | 8.732 | 8.524 | 8.197 |
| No | 14.457 | 15.219 | 9.661 | 9.573 | 8.225 | |
| t and ch | Yes | 32.260 | 33.161 | 19.924 | 19.808 | 16.535 |
| No | 32.260 | 33.174 | 25.516 | 19.808 | 16.936 | |
| n and ny | Yes | 20.543 | 19.766 | 17.746 | 22.503 | 17.158 |
| No | 20.543 | 20.843 | 19.930 | 22.503 | 16.753 | |
| h and hy | Yes | 16.274 | 16.653 | 19.566 | 20.051 | 19.144 |
| No | 16.274 | 15.680 | 19.999 | 20.051 | 19.283 | |
| m and my | Yes | 17.785 | 17.476 | 21.077 | 31.808 | 17.221 |
| No | 17.785 | 17.662 | 28.470 | 31.808 | 16.612 | |
| r and ry | Yes | 24.411 | 23.711 | 23.000 | 33.354 | 16.881 |
| No | 24.411 | 24.975 | 33.116 | 33.354 | 17.244 | |
| g and gy | Yes | 29.372 | 29.965 | 30.519 | 35.654 | 24.537 |
| No | 29.372 | 30.224 | 32.974 | 35.564 | 26.450 | |
| z and j | Yes | 20.181 | 21.856 | 13.346 | 12.832 | 14.301 |
| No | 20.181 | 21.432 | 12.285 | 12.240 | 14.283 | |
| d and dy | Yes | 24.117 | 25.072 | 32.348 | 36.396 | 30.713 |
| No | 24.117 | 24.881 | 33.124 | 36.396 | 30.334 | |
| b and by | Yes | 26.167 | 25.598 | 30.720 | 38.011 | 18.560 |
| No | 26.167 | 26.355 | 35.903 | 38.011 | 17.997 | |
| p and py | Yes | 36.408 | 36.360 | 41.714 | 43.460 | 33.970 |
| No | 36.480 | 36.793 | 43.740 | 43.460 | 33.290 |
In the experiment results of Appendix 1, accuracy improvement was observed for phonemes with low occurrence frequency in the training data. Therefore, when switching from one-hot label prediction to phoneme feature prediction, improvement in the accuracy of phonemes with low occurrence frequency should also be confirmed.
In this section, we calculated the accuracy for each phoneme using the network used in the experiment section. This experiment also used phoneme alignment data inferred by the Viterbi algorithm with a minimum allocation of 50 milliseconds for comparison. The comparison results with the model trained without one-hot label rewriting are as follows.
As can be seen from Figure 4, the accuracy for less frequent phonemes improved, and especially for “dy” and “v”, the accuracy improved with learning using phoneme features. From the above, it can be inferred that applying phoneme alignment to consonants with low occurrence frequency in the training data makes it closer to human labeling.