Dwango Media Village(ドワンゴメディアヴィレッジ,dmv)

深層学習モデルをアプリケーションなどに組み込む需要が増えてきています。しかしながら、深層学習モデルは従来の機械学習モデルと比べデータサイズが巨大となることが多く、ネットワーク経由でアプリケーションを配布する場合などに問題となります。そのため、学習済みの深層学習モデルを精度を落とさないように圧縮し、データサイズを削減する モデル圧縮（Model Compression [Bucilua2006] という技術が研究されつつあります。

本ドキュメントでは、モデル圧縮の手法についてサーベイし概観できるように分類しまとめたものになります。

とりあえず試してみたい方のために、簡単にモデル圧縮を試すことができるKeras向けのコマンドラインツール keras_compressor を実装しました。このツールは実装の容易な行列分解とテンソル分解を用いたモデル圧縮を行います。典型的な画像処理タスクにおいて、モデルから精度を0.1%しか落とさずにモデルのパラメータ数を6分の1以下に減らすことができました。

ドワンゴメディアヴィレッジでインターンをしている草野 (cocuh) が、インターンの一環として本ドキュメントを書きました。ドワンゴメディアヴィレッジはドワンゴの機械学習技術の研究開発部署です。

keras_compressor

具体的な手法を紹介する前に、どの程度モデルを圧縮できるかの実験を行います。今回、我々は実装が簡単な #[i 行列分解] （SVD,Tucker分解）を用いモデル圧縮を行うツール keras_compressor をKerasに向けに実装しました。これらの手法を選択した理由は2つあり、他の手法と比べ実装が容易であり深層学習フレームワークに大きな変更を加えず実装できるためと、圧縮時に訓練データセットを必要とせずモデルさえ与えれば圧縮できるためツールとして有用であるためです。

このツールは学習済みモデルと許容誤差パラメータを与えると、許容誤差範囲内で可能な限り圧縮を行いパラメータ数を削減したモデルを出力します。許容誤差パラメータは、モデルの精度とデータサイズのバランスを調整しているパラメータで、内部的には圧縮後のパラメータと圧縮前のパラメータの平均誤差の上界です。許容誤差を大きくするとデータサイズは削減されますが精度が落ちます。内部の詳しいアルゴリズムの説明は省略しますが、内部的に分割統治法や二分探索を使い制約付き離散最適化問題を解いています。

下のようなコマンドを実行すると圧縮したモデルを出力してくれます。

python keras_compressor.py --error=0.01 model.h5 compressed.h5

実験

実験をMNISTとCIFAR10を用いて学習したモデルを圧縮して、パラメータ数と精度（test accuracy）を評価します。MNISTで用いるモデルのネットワーク構造は、Kerasのexample code にあるものを実験に用います。このモデルは2層の畳み込み層と2層の全結合層からなります。

CIFAR10で用いるモデルのネットワーク構造は、Torchのblogで紹介されているものを実験に用います。このモデルは13層の畳み込み層と2層の全結合層からなります。

実験コードは、keras_compressorのレポジトリのexampleディレクトリに同封してあるので、再実験したい方は以下のコマンドを実行するとできます。下のコマンドで再実験した実験結果が、異なる場合があります。これは、学習されたモデルのパラメータが深層学習の訓練時のランダムネスにより異なった値となり、圧縮しやすさが異なるためです。

git clone https://github.com/nico-opendata/keras_compressor
cd ./keras_compressor
pip install --upgrade .
cd ./keras_compressor/example/mnist
python train.py
python compress.py
python finetune.py
python evaluate.py model_raw.py
python evaluate.py model_compressed.py
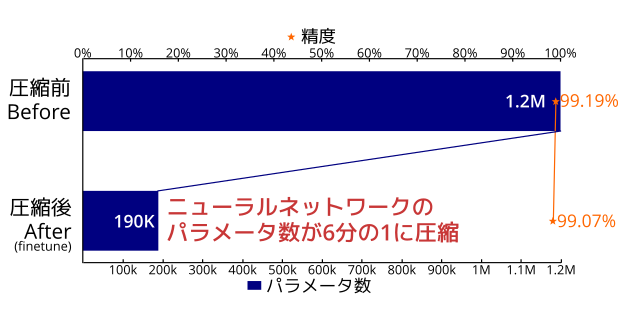
python evaluate.py model_finetuned.py

実験結果

MNIST

MNISTで学習したモデルを許容誤差パラメータ0.7で圧縮したところ、84.19%のパラメータを削減することができました。圧縮による精度悪化は5%（99.19%→94.95%）となり、finetuningを行うと精度悪化は0.12%（99.19%→99.07%）となり軽減されました。

保存されたモデルのデータサイズも、圧縮前は4,825KBだったものが圧縮後は756KBとなり、本ツールはモデルを圧縮できることを確認できました。

CIFAR10

CIFAR10で学習したモデルを許容誤差パラメータ0.3で圧縮したところ、54.58%のパラメータを削減することができました。圧縮による精度悪化は25.29%（91.22%→65.93%）とかなり悪化しましたが、finetuningを行うと精度悪化は0.19%（91.22%→91.03%）と許容できる程度となりました。

保存されたモデルのデータサイズも、圧縮前は58MBだったものが圧縮後には27MBとなり、CIFAR10においても本ツールはモデルを圧縮することができることが確認できました。

結論

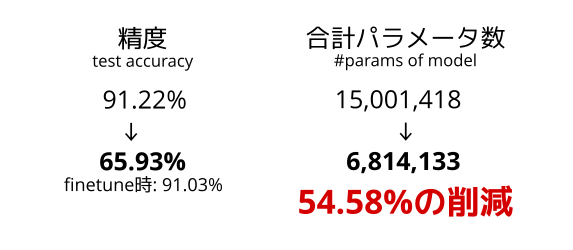
行列分解によるモデル圧縮により、場合によってはモデルのデータサイズを6分の1以下に圧縮できることを示しました。圧縮による精度悪化もサービスによっては許容できる範囲内だと考えられます。加えて、我々の開発したkeras_compressorでモデルが圧縮できることも示せました。

次節では、モデル圧縮の各手法について論文を参照しながら紹介します。

モデル圧縮の重要性

深層学習モデルは、従来の機械学習モデルと比べモデル自体のデータサイズが大きくなることが多いです。この巨大なデータサイズは以下のようなときに問題となります。

学習済みモデルを配布する場合

サービスや研究目的で学習済みモデルをネットワーク経由で配布する場合があります。たとえば、物体識別をするスマートフォンアプリを作りたいとします。Kerasで配布している物体識別モデル VGG19+ImageNet はデータサイズが548MByteあり、ネットワーク経由で通信しスマートフォンで扱うには大きすぎます。この場合、多少アプリの精度が悪くなってもデータサイズを圧縮して、通信時間や配布コストを減らしたいという欲求が生まれます。

分散環境で学習を行なう場合

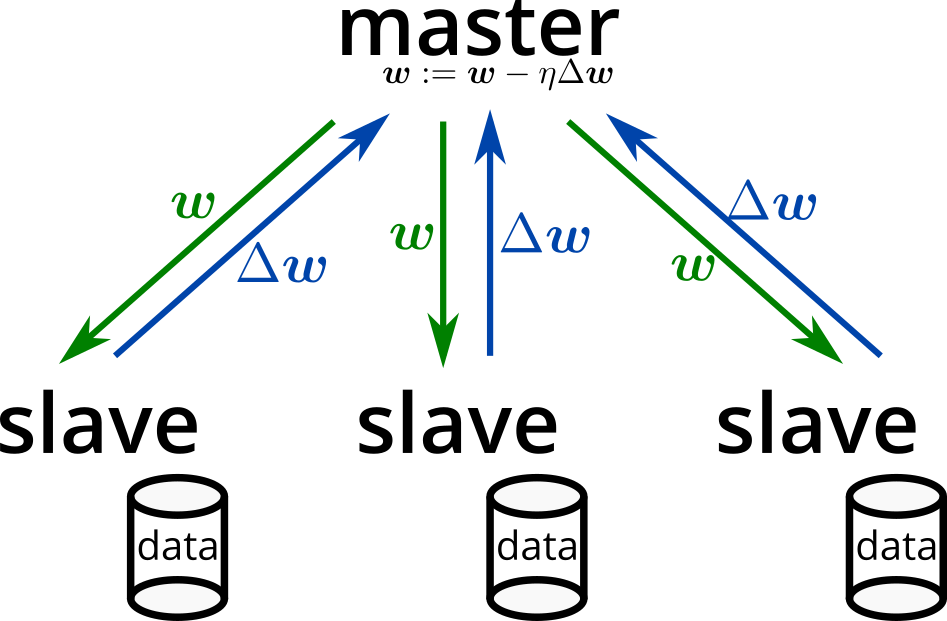
分散環境で深層学習モデルを学習させる 分散深層学習（distributed deep learning） [Dean2012] という技術があります。実装としては、ChainerMNやDistributed TensorFlowなどがあります。最近では、データを集約するとデータ漏洩やプライバシーの問題になりうると指摘があり [WhiteHouse2013]、データを集約せず利用者の計算資源を使った分散学習も注目されています [Google2017]。

分散学習（特にデータ並列型のSGD）は、モデルのパラメータの値や勾配を同期しながら学習を行うため、モデルのデータサイズが巨大である場合、それらの同期の通信がボトルネックとなり得ます。このため、モデル圧縮による通信コスト削減が、学習時間の削減につながると期待されています。

深層学習のモデル圧縮の重要性

モデル圧縮の手法

モデル圧縮（model compression）[Bucilua2006] は、学習済みのモデルのデータサイズを削減を目的とする手法です。そのため、多くの手法があり実運用する上では各手法の違いと特徴を理解する必要があります。

本ドキュメントにおいては、モデル圧縮の各手法を3つのカテゴリに分け紹介します。モデル圧縮の手法を分類したものはあまりなく、下の分類は本ドキュメントの筆者が行ったものです。また、学習時から小さいモデルを利用し学習することは small-footprint network [Sindhwani2015] などと呼び、model compressionとは違った技術であるとし、本ドキュメントではあまり触れません。

各層を個別に圧縮する手法（layer-wise compression）
- structured matrix [Sindhwani2015] [Denil2013]
- matrix factorization [Denil2013]
- tensor factorization [Kim2015]
- weight sharing [Han2015] [Chen2015]
- sparse connection [Sun2016]
モデル全体を小さいモデルに再学習する（model-wise compression）
- distillation [Hinton2015]
- mimic learning [Bucilua2006]
モデルのシリアライズを工夫する（serialization）
- sparse matrix [Han2015]
- haffman coding [Han2015]
- fixed point number, int8 [Lin2016]

各層を個別に圧縮する手法（layer-wise compression）

深層学習モデルは一般に複数の層からなり、各層は行列やテンソルで記述されたアフィン変換と活性化関数による非線形変換からなります。この各層の行列やテンソルがモデルのデータサイズの大半を占めているため、行列やテンソルを圧縮しようというのが、layer-wise compressionです。

layer-wise compressionの利点として、学習済みモデルの構造をそのまま再利用するため、新たな手間をかけずに比較的容易に行うことができます。しかしながら構造を再利用するため、圧縮後のモデルの深さは圧縮前のモデルの深さより小さくなることはありません。このため、一般にレイテンシーも圧縮前と同等もしくは悪化することが予想されます。

layer-wise compressionとして、最もよく使われる考え方はstructured matrixです。$N\times M$行列を記述するためには$NM$個のパラメータが必要となりますが、なんらかの構造（低ランク性など）を盛り込むことにより$NM$個未満のパラメータで表現しようとすることです。具体的な手法として、**行列分解（matrix factorization）とテンソル分解（tensor factorization）とパラメータの共通化（weight sharing）**を取り上げます。

行列分解（matrix factorization）

行列分解とは、 $N\times M$行列 $\mathbf{W}$が与えられたときに、$N\times K$行列 $\mathbf{U}$と $K\times M$行列 $\mathbf{V}$に分解することです。 $\mathbf{W}$を表現するには$NM$個のパラメータで表現していたものを、$\mathbf{U}, \mathbf{V}$で表現できれば$NK+KM$個のパラメータで $\mathbf{W}$を表現できたといえ、 $K$が十分に小さければ少ないパラメータで $\mathbf{W}$を表現できたといえます。

深層学習のモデル圧縮の手法(行列分解)

\[ A \simeq UV\\ U\in\mathbb{R}^{N\times K}\\ V\in\mathbb{R}^{K\times M}\\ \]

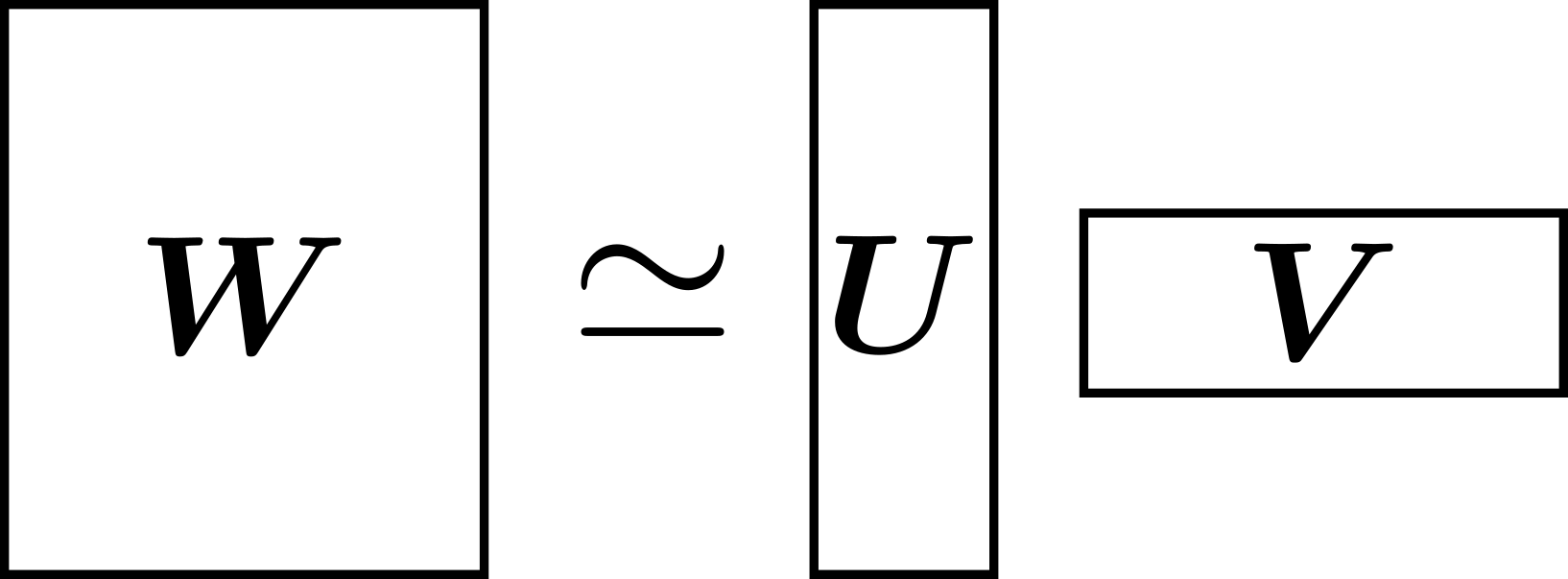
$\mathbf{W}$を小さい $K$で $U,V$に近似する手法の一つとして、低ランク近似が挙げられ情報推薦などで使われています。低ランク近似と呼ばれるように$\mathbf{W}$が低ランクであることを仮定しています。このため $\mathbf{W}$が低ランクでない場合は圧縮しても精度が悪くなることがありえます。

この手法の実装は比較的容易で、1つの全結合層を2つの全結合層に置換すればよいです。このとき、2つの全結合層のうち入力層に近い方の活性化関数は何も指定しません。既存の深層学習フレームワークにそのまま載るため、汎用的に使うことができます。前述の keras_compressor ではこちらを実装しています。

\[ \sigma(Ax + b) \sim \sigma(U(Vx) + b) \]

テンソル分解（tensor factorization）

前節で、行列分解について述べましたが、この考え方はテンソルにおいてもそのまま転用することができます。テンソルの低ランク近似の手法として（CP分解やTucker分解など）があります。

よく使われるTucker分解（tucker decomposition）について解説します。Tucker分解は、与えられたテンソルをある軸を基準に行列とテンソルに分解します。下図では、3つある軸すべてに対して分解を行い、3次テンソル $\mathcal{W}$ を3次テンソル $\mathcal{C}$ と行列 $\mathbf{U_1, U_2, U_3}$ に分解しています。

深層学習のモデル圧縮の手法(テンソル分解)

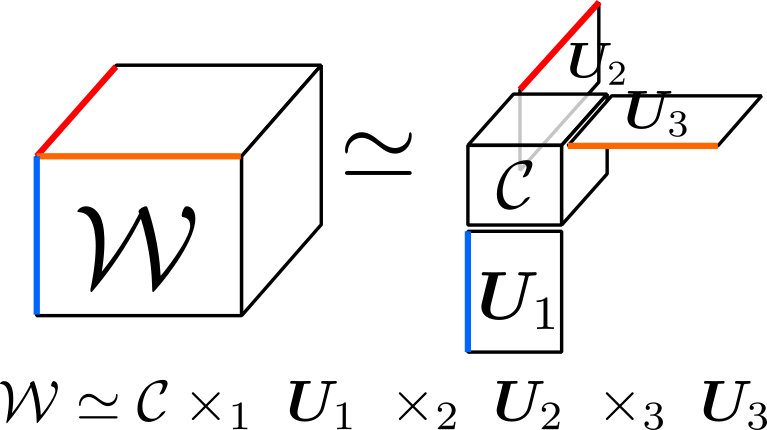
畳み込み層をTucker分解を行う場合について議論します。$H\times W$ の窓を持ち入力チャンネル $C_\text{in}$ で出力チャンネル $C_\text{out}$ となる畳み込み層を考えます。この畳み込み層のカーネルは4次テンソルになり、 $\mathcal{W}\in\mathbb{R}^{H\times W\times C_\text{in}\times C_\text{out}}$ と書くことにします。これを入力チャンネル方向 $C_\text{in}$ と出力チャンネル $C_\text{out}$ 方向にTucker分解します（下式）。

\[ \mathcal{W}\simeq \mathcal{C}\times_3\mathbf{U}_\text{in}\times_4\mathbf{U}_\text{out} \]

target tensor: $\mathcal{W}\in\mathbb{R}^{H\times W\times C_\text{in}\times C_\text{out}}$
core tensor: $\mathcal{C}\in\mathbb{R}^{H\times W\times K_\text{in}\times K_\text{out}}$
factor matrix: $\mathbf{U}_\text{in}\in\mathbb{R}^{K_\text{in}\times C_\text{in}}$, $\mathbf{U}_\text{out}\in\mathbb{R}^{K_\text{out}\times C_\text{out}}$

このときのパラメータ数が

\[ \mathop{size}(\mathcal{W})\gg\mathop{size}(\mathcal{C})+ \mathop{size}(\mathbf{U}_\text{in})+ \mathop{size}(\mathbf{U}_\text{out}) \]\[ HWC_\text{in}C_\text{out}\gg HWK_\text{in}K_\text{out}+ K_\text{in}C_\text{in}+L_\text{in}C_\text{in} \]

となるように、$K_\text{in}$, $K_\text{out}$ を設定すればパラメータ数が削減できたといえます。

このTucker分解がうまくいく場合は、簡単に言えば圧縮する方向に低ランクである場合、つまり似たようなフィルタを適用している場合です。そのため、似ていない異なるフィルタ（他のフィルタの線形和で表現できないフィルタを用いている場合）はTucker分解の近似精度が悪くなり、圧縮後のモデルの精度も悪化します。

また、畳み込み層の圧縮ではチャンネル方向（$C_\text{in}$, $C_\text{out}$）に対してのみTucker分解を適用し、縦横方向（$H,W$）には一般的に適用しません。これは、$H,W$は3や5など小さい値であるので圧縮するメリットがないためと、縦横方向に似たような係数がなく低ランクとならないことが多いためです。

この手法の実装も簡単で、1つの畳み込み層$L$を3つの畳み込み層$L_\text{in}$, $L_\text{core}$, $L_\text{out}$に置き換えれば良いです。このとき、各層は

$L_\text{in}$: $1\times 1$ の畳み込み層、出力チャンネルは $K_\text{in}$、係数は $\mathbf{U}_\text{in}$ を変形したもの
$L_\text{core}$: $H\times W$ の畳み込み層、出力チャンネルは $K_\text{out}$、係数は $\mathcal{C}$
$L_\text{out}$: $1\times 1$ の畳み込み層、出力チャンネルは $C_\text{out}$、係数は $\mathbf{U}_\text{out}$ を変形したもの

となります。

\[ L(\mathbf{x})\simeq L_\text{out}\circ L_\text{core}\circ L_\text{in}(\mathbf{x}) \]

この手法では、ネットワークの係数を共通化することによりパラメータ数を削減します。たとえば、畳み込み層は出力画素ごとに係数を共通化しているため、全結合層と比べ少ないパラメータで巨大な出力を得る事ができます。

深層学習のモデル圧縮の手法(係数の共通化)

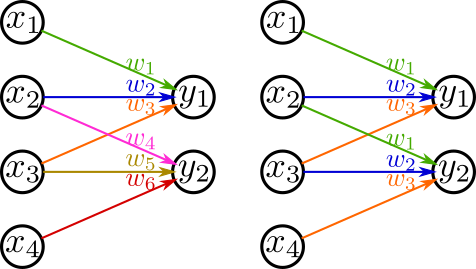
Hanらは係数行列 $\mathbf{W}$ の要素をクラスタリングし、クラスタ内で重みを共通化する手法を提案しました [Han2015] 。この手法では、クラスタ内での重みを共通化することにより、 $\mathbf{W}$ を各要素のクラスタを示す整数行列 $\mathbf{A}$ と各クラスタの値を示すベクトル $\mathbf{v}$ で表現します。たとえば、 $\mathbf{W}$ の要素をクラスタリングしたとき、 $W_{1,1}$ の値がクラスタ3に入るのであれば、 $A_{1,1}$ は3となり、クラスタ3の平均が0.4ならば $v_3=0.4$ となります。この手法のみではパラメータ数を削減することはできないですが、$\mathbf{A}$ をint8で表現するなどのシリアライズの工夫と組み合わせることによりデータサイズの削減をすることができます。

モデル全体を小さいモデルに再学習する（model-wise compression）

Hintonらが提案した 蒸留（distillation） という手法があり、この手法は与えられた巨大な学習済みモデルと同じ挙動をするデータサイズの小さいモデルを学習させる手法です [Hinton2015] 。この蒸留という手法は、Bucilaらの提案したmimic learningという手法を元にしています。mimic learningはrandom forestやboostingなどを用いた巨大なモデルを圧縮する手法で、これを分類問題を扱う深層学習モデル（特にアンサンブル学習などをしているモデル）に適用したのがdistillationです。

これらの手法は、 教師モデル $f$ と 生徒モデル $g$ を考えます。教師モデルは学習済みモデルであり十分に巨大なネットワークであるとします。生徒モデルは教師モデルと同様の出力をするように学習させます。GANなどと異なり、生徒モデルが学習している間、教師モデルは変化しません。

本質的には以下の問題を解くこととなり、データ生成分布 $p$ について期待損失を最小化します。$l$ は損失関数で、分類であればcross entropy損失、回帰であれば二乗損失などとなります。

\[ \mathrm{minimize}_g E_{x\sim p}[l(f(x), g(x))] \]

この手法の利点は、教師モデルのネットワーク構造が生徒モデルのネットワーク構造に影響しないことです。そのため、layer-wiseの場合はできなかった層を減らすという圧縮ができ、レイテンシーの改善が期待できます。また、データ生成分布 $p$ についての期待値を近似できれば良いため、$g$ を学習する際の訓練データにラベルデータは必要ありません、$f(x)$ をラベルとして使うためです。欠点としては、生徒モデル $g$ のネットワーク構造を設定する必要があり、目的の精度を達成する生徒モデルを試行錯誤により得る必要があります。

distillationの特徴的なこととして、教師モデルと生徒モデルの最終層がsoftmax層であるとき、両方のsoftmax層に温度 $T$ を導入して学習を行うことです。$T$ を大きい値に設定すると、教師モデルの出力が0や1に偏ってないベクトル、ソフトなラベルを出力するようになります。このラベルを教師データとして用いることによりソフトラベル（soft target）を利用することとおなじ効果が得られ、生徒モデルが教師モデルから受け取る情報が増え汎化性能や収束速度が向上します。$T$ を大きい値に設定するのは、生徒モデルを学習させているときのみで、予測時は$T=1$に設定し通常のsoftmax層と同じ関数を使います。

\[ \sigma(\mathbf{z}; T)_i=\frac{\exp(z_i/T)}{\sum_{k=1}^K\exp(z_k/T)} \]

モデルのシリアライズを工夫する

モデルの構造やパラメータを変えずにデータサイズを削減する方法として、行列やテンソルをバイナリデータに変換する際のシリアライズを工夫する方法があります。ここでは、sparse matrix format と 量子化（quantization） について取り上げます。

sparse matrix format

$N \times M$ のfloat32の行列 $\mathbf{W}$ をナイーブに保存すると32NM bit必要となりますが、行列 $\mathbf{W}$ がスパースであるならば座標と値のタプルとして保存したほうがサイズを小さくできます。たとえば、

\[ \mathbf{W} = \begin{pmatrix}0&0&0.3&0.4\\0.1&0&0&0\\0&0.2&0&0\end{pmatrix} \]

である場合、座標と値のタプルの集合で示すと

\[ \left\{((1,3), 0.3),((1,4), 0.4),((2,0), 0.1),((3,2), 0.2)\right\} \]

となります。各座標をuint8で各値をfloat32で示すと一つのタプルは$8 \times 2 + 32 = 48$ bitとなり、集合で表現したほうは$48 \times 4 = 192$ bit、ナイーブに表現すると$32 \times 4 \times 4 = 512$ bitとなるためよりデータサイズを小さく表現できたといえます。

このように、疎行行列（sparse matrix）は座標と値のタプルで表現するほうがデータサイズを削減できることが多く、そのようなエンコード方法をsparse matrix storage formatなどといいます。

この手法を実装するのは比較的難しいです。理由は、sparse matrixをサポートしているライブラリが少ないためです。特に、GPU計算をサポートしている深層学習ライブラリはほぼないです（2017/5現在）。そのためGPUを用いたい場合は、ディスクにsparse matrixとして保管し使用する時はdense matrixとしてGPUメモリーに展開するのが現状良いと思われます。

量子化（quantization）

一般に深層学習モデルの係数は単精度浮動小数点数（float32）を用いられますが、これを固定小数点数を用いint8やint16などに量子化することでモデルのデータサイズを半分や4分の1にすることができます。また、量子化しても性能悪化があまりおこらないことが報告されています [Lin2016] 。さらに、計算時間に関しても浮動小数点数より固定小数点数のほうが早く計算できるため、レイテンシーの改善が見込まれます。

実装に関して、深層学習フレームワークの多くは浮動小数点数を前提に実装されており、固定小数点数をサポートしているフレームワークはあまりありません（2017/5現在）。自分で実装する際は、フレームワークによると思いますが、自分で固定小数点数型の係数を使う層を実装する必要があります。手法としてはかなり簡単であるため、今後フレームワークに実装さえされれば、すぐにでも普及するモデル圧縮と考えられます。

まとめ

これまで紹介したように、モデル圧縮は多くの手法が研究開発されています。しかしながら、モデル圧縮に関する実装や実アプリケーションでの応用はあまりされていません。実装や応用の先駆けとして、我々はKeras向けのモデル圧縮を行うコマンドラインツールを開発し、実験を行いました。

今後、深層学習が普及するためには実用に堪えうるモデル圧縮の実装とノウハウが必要とされると思います。サーベイを行う中で、多くの手法はライブラリに実装されておらず、容易に利用可能ではないことが課題であると感じました。この資料を読んで、モデル圧縮に興味を持ってくださると幸いです。

もし実用に興味があり論文を読みたい方には、 [Kim2015] と [Han2015] から読むことをおすすめします。

参考文献

[Bucilua2006] Cristian Buciluˇa, Rich Caruana, and Alexandru Niculescu-Mizil. Model compression. In Proceedings of the 12th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, KDD’06, pp. 535–541, New York, NY, USA, 2006. ACM. https://www.cs.cornell.edu/~caruana/compression.kdd06.pdf

[Dean2012] Jeffrey Dean, Greg S. Corrado, Rajat Monga, Kai Chen, Matthieu Devin, Quoc V. Le, Mark Z. Mao, Marc’Aurelio Ranzato, Andrew Senior, Paul Tucker, Ke Yang, and Andrew Y. Ng. Large scale distributed deep networks. In Proceedings of the 25th International Conference on Neural Information Processing Systems, NIPS’12, pp. 1223–1231, USA, 2012. Curran Associates Inc. https://papers.nips.cc/paper/4687-large-scale-distributed-deep-networks

[Sindhwani2015] Vikas Sindhwani, Tara Sainath, and Sanjiv Kumar. Structured transforms for small-footprint deep learning. In C. Cortes, N. D. Lawrence, D. D. Lee, M. Sugiyama, and R. Garnett, editors, Advances in Neural Information Processing Systems 28, pp. 3088–3096. Curran Associates, Inc., 2015. https://papers.nips.cc/paper/5869-structured-transforms-for-small-footprint-deep-learning

[Denil2013] Misha Denil, Babak Shakibi, Laurent Dinh, Marc’ Aurelio Ranzato, and Nando de Freitas. Predicting parameters in deep learning. In C. J. C. Burges, L. Bottou, M. Welling, Z. Ghahramani, and K. Q. Weinberger, editors, Advances in Neural Information Processing Systems 26, pp. 2148–2156. Curran Associates, Inc., 2013. https://papers.nips.cc/paper/5025-predicting-parameters-in-deep-learning

[Kim2015] Yong-Deok Kim, Eunhyeok Park, Sungjoo Yoo, Taelim Choi, Lu Yang, and Dongjun Shin. Compression of deep convolutional neural networks for fast and low power mobile applications. CoRR, Vol. abs/1511.06530, 2015. https://arxiv.org/abs/1511.06530

[Chen2015] W. Chen, J. T. Wilson, S. Tyree, K. Q. Weinberger, and Y. Chen. Compressing Neural Networks with the Hashing Trick. ArXiv e-prints, April 2015. https://arxiv.org/abs/1504.04788

[Han2015] Song Han, Huizi Mao, and William J. Dally. Deep compression: Compressing deep neural network with pruning, trained quantization and huffman coding. CoRR, Vol. abs/1510.00149, , 2015. https://arxiv.org/abs/1510.00149

[Sun2016] Y. Sun, X. Wang, and X. Tang. Sparsifying neural network connections for face recognition. In 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), pp. 4856–4864, June 2016. https://arxiv.org/abs/1512.01891

[Hinton2015] G. Hinton, O. Vinyals, and J. Dean. Distilling the Knowledge in a Neural Network. ArXiv e-prints, March 2015. https://arxiv.org/abs/1503.02531

[Lin2016] Darryl D. Lin, Sachin S. Talathi, and V. Sreekanth Annapureddy. Fixed point quantization of deep convolutional networks. In Proceedings of the 33rd International Conference on International Conference on Machine Learning - Volume 48, ICML’16, pp. 2849–2858. JMLR.org, 2016. https://arxiv.org/abs/1511.06393

[Google2017] Research Blog: Federated Learning: Collaborative Machine Learning without Centralized Training Data. https://research.googleblog.com/2017/04/federated-learning-collaborative.html

[WhiteHouse2013] White House Report. Consumer data privacy in a networked world: A framework for protecting privacy and promoting innovation in the global digital economy. Journal of Privacy and Confidentiality, 2013. http://repository.cmu.edu/jpc/vol4/iss2/5/

Author

Publish: 2017/05/19

Kosuke Kusano

深層学習のモデル圧縮