

ニコニコ静画(イラスト)に投稿された175万枚の画像を用いて、閲覧数とお気に入り数を予測する回帰の問題としてChainerを用いて学習させました。
モデルの全体的な構造は GoogLeNet [1] をベースにしたものです。元になっているGoogLeNetの構造は下図のようになっています。
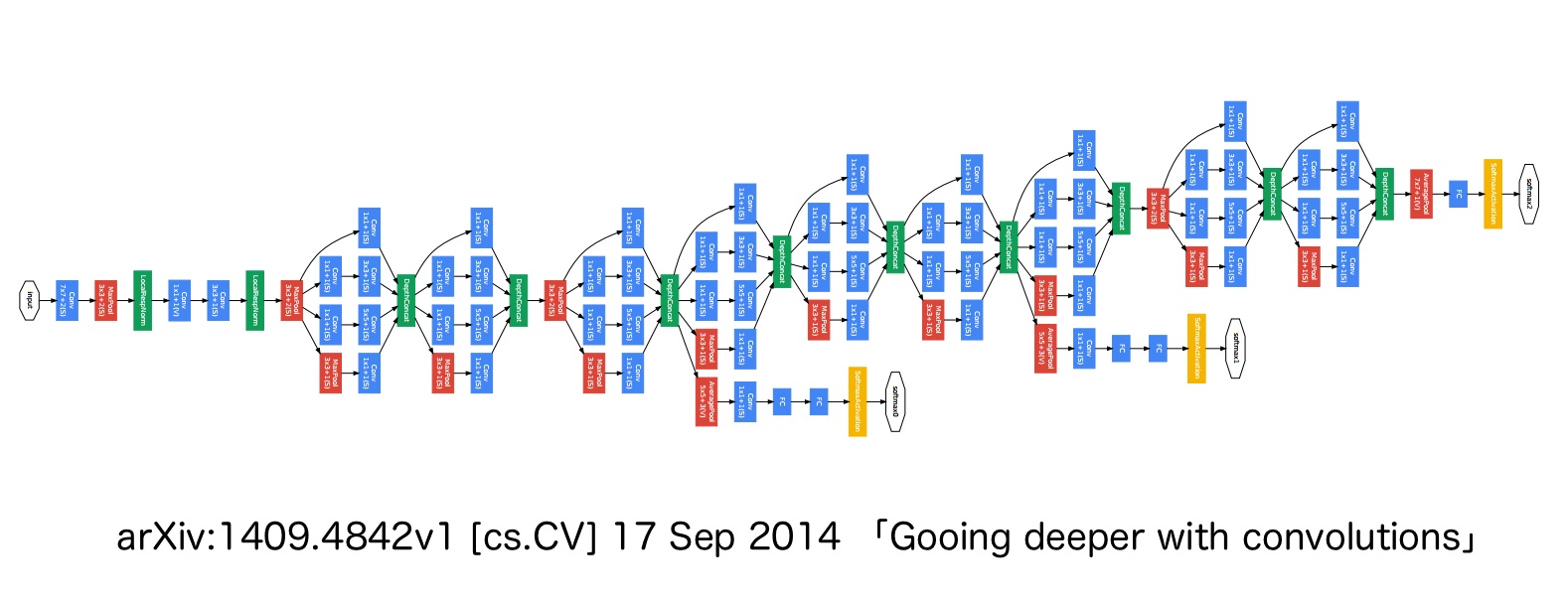
高速化や精度向上等のため、Batch Normalization [2] を各層に加え、各活性化関数の手前でミニバッチの正規化を行うようにしています。元のネットワークはクラス識別問題用のネットワークになっていますが、Softmax関数の交差エントロピーを誤差関数としている箇所を平均二乗誤差を誤差関数とすることで、回帰問題に対応します。
オプティマイザは、Adam/AdaGrad/AdaDeltaを学習の途中で確率的にランダムで切り替えることにしました。これまでに幾つかのタスクで検証した所、途中でオプティマイザをランダムに切り替えた場合でも、最終的には、最適に設定したオプティマイザと同じ程度の精度が出ていたため、このアプローチを選択しました。Chainerを利用すれば、このように動的に学習を変えることは容易です。
タスクとしては閲覧数とお気に入り数そのものを予測したいわけですが、最適化の対象とする誤差関数は「log(閲覧数+定数)の平均二乗誤差とlog(お気に入り数+定数)の平均二乗誤差の和の平均」としました。学習時の誤差関数として、閲覧数の素の値の平均二乗誤差を使う場合、閲覧数10を100と予想した誤差よりも、閲覧数10,000を10,100と予想した時の誤差が大きくなってしまいます。実際に、誤差関数を閲覧数・お気に入り数の素の値について平均二乗誤差とした場合、閲覧数が数万クラスの一部の画像の誤差に引っ張られて、閲覧数の桁が少ない画像についてなかなか学習が進まないという状況になります。「何桁ぐらいの閲覧数が得られそうかを予測する」(→100閲覧と1,000閲覧の誤差の重みは、1,000閲覧と10,000閲覧の誤差と同じぐらい)というのが学習の仕方として良さそうなので、logスケールで学習することとしました。
学習に使わなかった5000枚のイラストに対して、予測値再生数と実際の再生数をそれぞれ横軸/縦軸としてプロット(logスケール)すると、以下のような結果になります。各点は、イラストそのものでプロットしています。
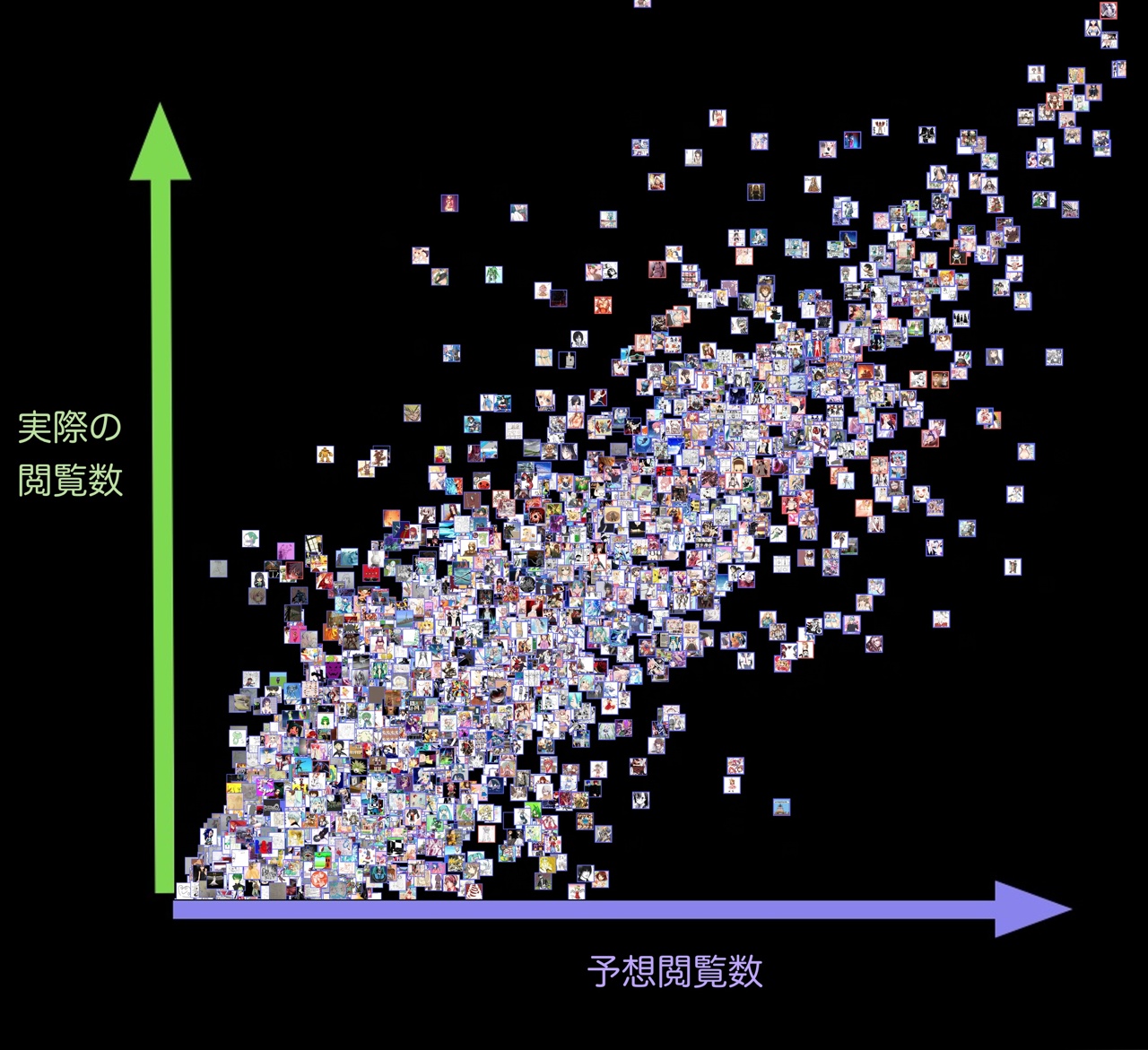
左上、右下にはほとんど点が出ておらず、予測値はほぼ1桁以内の誤差に収まっており、このニューラルネットは少なくとも大量閲覧数を叩き出すヒット作品を見落とすようなことは無さそうです。
また、予想閲覧数と予想お気に入り数をプロットすると以下のようになります。
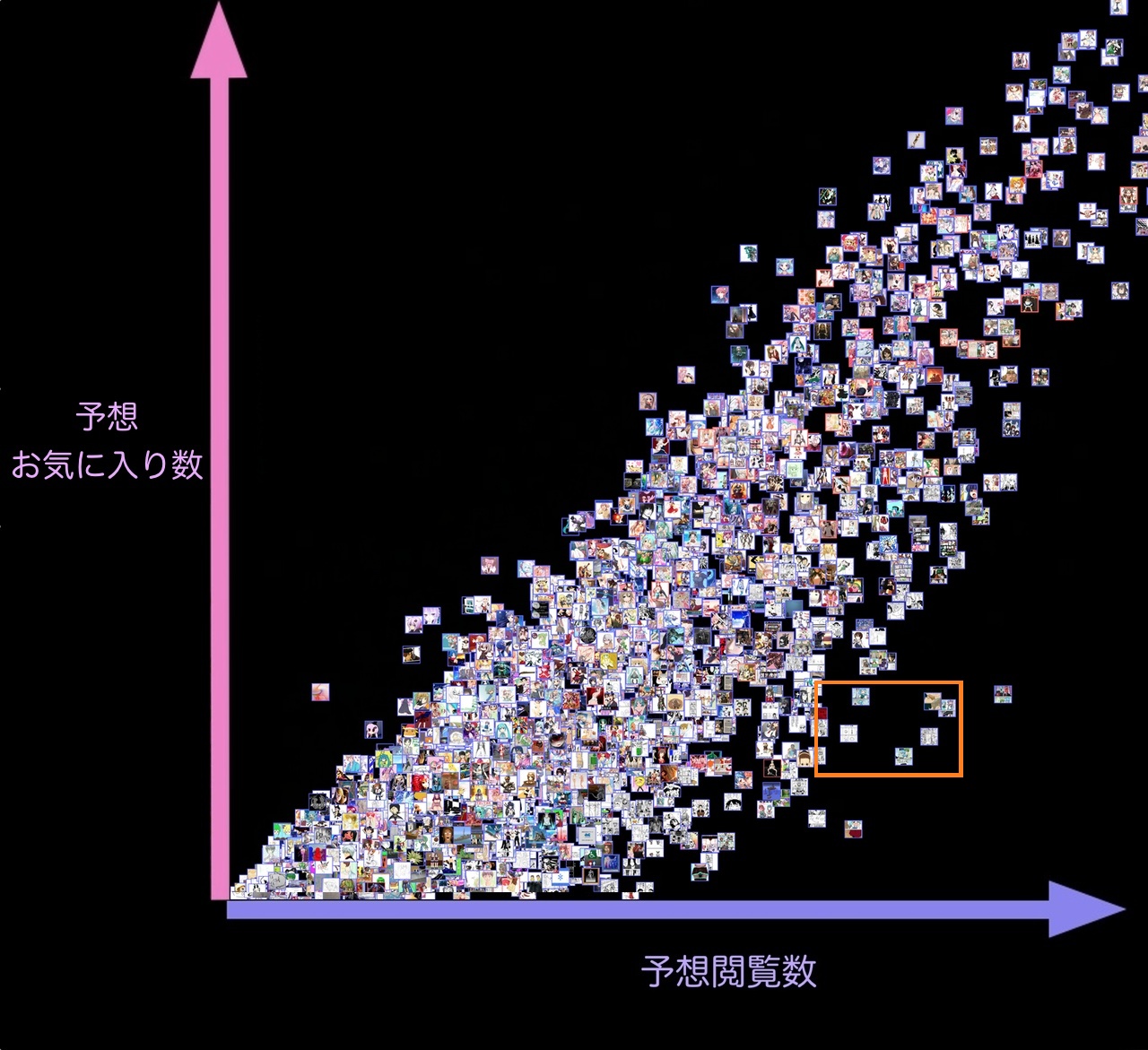
予想閲覧数と予想お気に入り数も、完全には一直線上には並んでいないので、「お気に入り数に対する閲覧数の割合が高そう(右下エリア)」のように、閲覧数とお気に入り数の評価は別々に評価していることが分かります。
数コマのマンガ形式で読ませるような作品は、お気に入り数に対する閲覧数の比率が高い傾向がある(サムネイル画像ではセリフ等が読めないため、実際に閲覧ページまで遷移しやすい)のですが、この傾向は掴めているでしょうか。下に、右下エリア(オレンジ色の点線範囲)を拡大したものを示します。
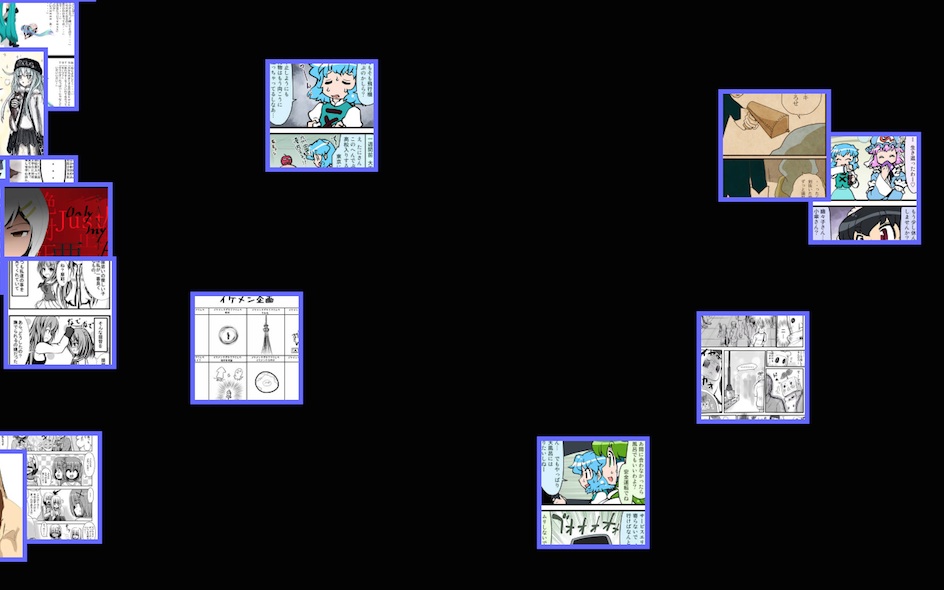
対角より右下にプロットされているこのエリアのイラストにはマンガ形式のものが多いことから、上記のような傾向も正しく学習できていることが分かります。
「絵の上手さ」は定義が難しく、主観的な要素も多分に含まれ直接的に測るのは難しいものですが、今回は「閲覧数/お気に入り数」を学習することにより、「ニコニコ静画での閲覧数/お気に入り数がどの程度得られるか」という問題に落とし込んで学習しました。
閲覧数を予測する場合、タグやタイトル検索の露出機会、SNS共有や作者名効果などの要因も多いはずですが、それらの効果も含め、画像そのものから学習されているということになります。同じ構造のモデルで、キャラクター/タグ識別もある程度できており、実際には、絵の上手さというよりは、ニコニコ静画において、人気のキャラクターが描かれているかどうかが閲覧数の寄与割合として大きそうに思います。ただ、「オリジナル」タグの付いている、二次創作ではないイラストの中にも予測値が高いイラストも一定数あるため、「ニコニコ内で人気の出そうな画風/タッチ」のような概念も一定程度は学習出来ていそうです。
今回は画像のみでどこまで出来るかを調べるため、タグ情報やタイトル情報は学習に使いませんでしたが、それらも入れたマルチモーダルのモデルに発展させ、精度を向上させることが可能です。
時系列な要素についても今回は組み込みませんでしたが、実際には人気ジャンルのトレンドが存在することを考慮することで、こちらも精度向上に繋げたり、トレンド自体を Long short-term memory のような系列情報で予測するようなアプローチも考えられます。実際のサービスの中でオンラインで学習し続けるモデルとする場合、learning rateをどのように調節していくのが良いか、考慮すべき点があります。
今後、このような技術をサービスに組み込む場合、クリエイターの方がイラストを投稿する際に、実際に公開する前に、画像のデータのみから、ある程度の精度で閲覧数・お気に入り数を予測することが出来ます。このことから、予想閲覧数・予想お気に入り数が上がるまで描き直して都度スコアのチェック出来るようにする等の、クリエイターの方の投稿支援へ利用が考えられます。画像内を複数のエリアに分けて、どの箇所がどの程度予測閲覧数に寄与しているかを提示することで、画像内のエリア別の出来栄えを示すことが出来るようになります。これを用いると、予測閲覧数が高くなるようなサムネイル画像領域の切り出しも実現することが出来ます。
[1] Szegedy, Christian, et al. "Going deeper with convolutions." Proceedings of the IEEE conference on computer vision and pattern recognition. 2015. https://www.cv-foundation.org/openaccess/content_cvpr_2015/html/Szegedy_Going_Deeper_With_2015_CVPR_paper.html
[2] Ioffe, Sergey, and Christian Szegedy. "Batch normalization: Accelerating deep network training by reducing internal covariate shift." International conference on machine learning. pmlr, 2015. https://proceedings.mlr.press/v37/ioffe15.html