This article is automatically translated.

The content of this article is fundamental research not directly related to the algorithm used in the Mahjong AI “NAGA” replay service.

Overview

To accurately perform simulations and policy sampling in Mahjong, which is an imperfect information game, it is necessary to estimate uncertain information. In particular, the opponent’s hand is information that significantly affects strategy, but it is generally difficult to determine its distribution by enumeration. Therefore, methods such as maximum likelihood estimation using autoregressive neural networks have been proposed as ways to estimate hands using machine learning from actual game data. However, to perform simulations, it is necessary not only to obtain the most plausible hand prediction but also to quickly generate hand samples that follow the actual dataset distribution. Therefore, by using a diffusion process model, which has recently attracted attention in image data, we propose a method to generate samples closer to the actual distribution with lower computational cost. General diffusion process models handle continuous data such as images and audio, but since Mahjong hands are discrete set data, we treated the hand as a continuous vector representation of the number of each tile type, making it possible to apply existing diffusion process model learning methods. Experiments using Mahjong game data from the online Mahjong site Tenhou showed that the distribution of the number of tiles with respect to the Shanten number is closer to the actual data compared to an autoregressive model using a Transformer. We also compare the occurrence rate of waiting tiles in the generated hands with those in the dataset and introduce specific examples of generation in certain situations.

Estimation of Opponent’s Hands in Mahjong

Mahjong is a popular game played worldwide, and various AI agents capable of automated play have been researched. Recent prominent approaches include deep reinforcement learning using large-scale human game data and self-play [Li et al. 2020, Fu et al. 2021a, Li et al. 2022, Zao et al. 2022]. However, in multi-player games like Mahjong, efficient learning might be possible through simulation-based exploration. For example, Counterfactual Regret Minimization [Zinkevich et al.] and Monte Carlo Tree Search-based value estimation [Mizukami et al.] allow for more precise approximations of values and policies considering the probabilistic nature of the game. However, since Mahjong is an imperfect information game that includes uncertain information such as the opponent’s hand and the remaining tiles, simulations need to calculate future states from the current situation, making it difficult to directly apply simulation. Additionally, since the variations in possible game states in Mahjong are vast, exhaustive simulations are challenging. Due to the difficulty of handling such uncertain information, specific sampling of uncertain information is avoided in Mahjong AI using deep reinforcement learning by constraining the policy’s latent space [Han et al.].

Among the uncertain information in Mahjong that significantly impacts the game outcome is the opponent’s hand. The hand can be probabilistically represented by combinations of tiles excluding known tiles such as the player’s own hand, discarded tiles, and called tiles. However, even this leaves many possible hand variations, making it difficult to determine specific distributions by enumeration. Therefore, existing hand estimation methods have proposed machine learning approaches using CRF [Nemoto et al.]. In particular, Transformers have recently gained attention for their high performance, learning sequences of tile tokens representing hands with the game state as conditional input via autoregression. [Ogami et al.] reported that hand candidates that match the actual data can be estimated using Beam Search with predictions from a Transformer model compared to random estimation. However, to perform accurate simulations, it is necessary to generate multiple hand samples that follow the dataset distribution, not just obtain the most plausible hand prediction. Additionally, autoregressive generation requires forward computation for the length of the opponent’s hand, leading to high computational cost.

Therefore, we propose a hand generation method using the diffusion process. Hand estimation can be considered a data generation problem conditioned on the game state, and diffusion process models have recently been frequently used for images and videos. Diffusion process models are methods where the process of noise being progressively added and diffused into the data is approximated by a neural network, known for stable learning and generating diverse and high-quality samples [Song et al.]. Additionally, since the sequence length of the diffusion process during generation can be determined independently of the length of the generated data, it can be generated with less computational cost compared to autoregressive models. However, existing diffusion process models primarily target continuous value vectors such as pixel values, while Mahjong hands are discrete set data. Methods like Bit Diffusion [Chen et al.] convert discrete values to continuous values using diffusion processes, but applications to variable-length set data like Mahjong hands have not been explored. Therefore, we represented the hand as a real-valued vector using the number of each tile type, enabling learning with existing diffusion process models. During generation, sampling is performed from the vector representation of the number of tiles to concrete hands while ensuring the number does not exceed the possible tile limits.

Learning Hand Generation Using Diffusion Process Model

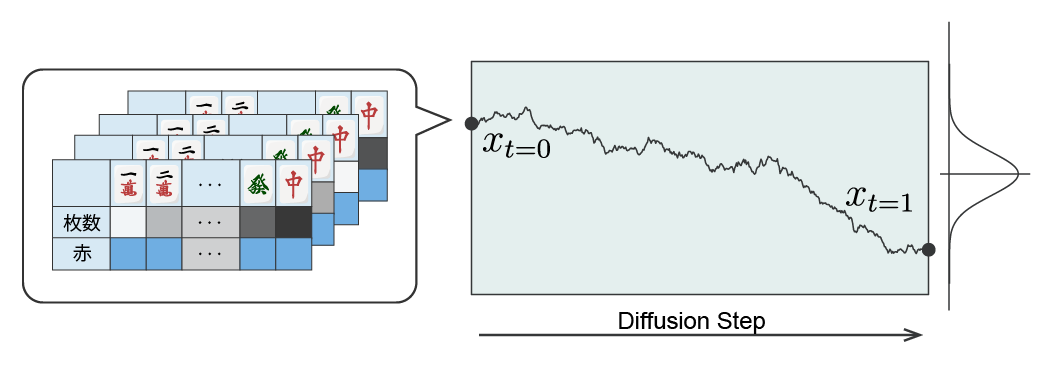
This study handles Japanese Reach Mahjong with four players, which is popular in Japan. The tiles in the game consist of 34 types with four tiles each, including red dora tiles. The proposed method generates an opponent’s hand from the certain information such as the wall, dora, point situation, and own hand from the perspective of one of the four players. The hand is variable-length data with different numbers of tiles depending on calls, and it is set data that does not change by rearranging the order of tiles. On the other hand, general diffusion process models handle fixed-length continuous vectors. Therefore, we represented the hand as a fixed-length continuous vector by the number of 34 tile types and the presence of red dora, and considered the diffusion process of this vector (Figure 1). Specifically, we transformed the possible tile counts \(\{0, 1, 2, 3\}\) to count reference points \(\{0, 0.25, 0.5, 0.75, 1\}\) linearly interpolated within the range \([0, 1]\), and combined a 34-dimensional vector indicating the presence of red tiles \(\{0, 1\}\) into a 2 x 34-dimensional vector for one player’s hand. This continuous value vector \(x\) of 4 x 2 x 34 dimensions, gathered for the four players including the subjective viewpoint of the generating player, is the generation target. Then, we considered the process of this vector diffusing into a standard normal distribution and learned the reverse process with a neural network \(f\).

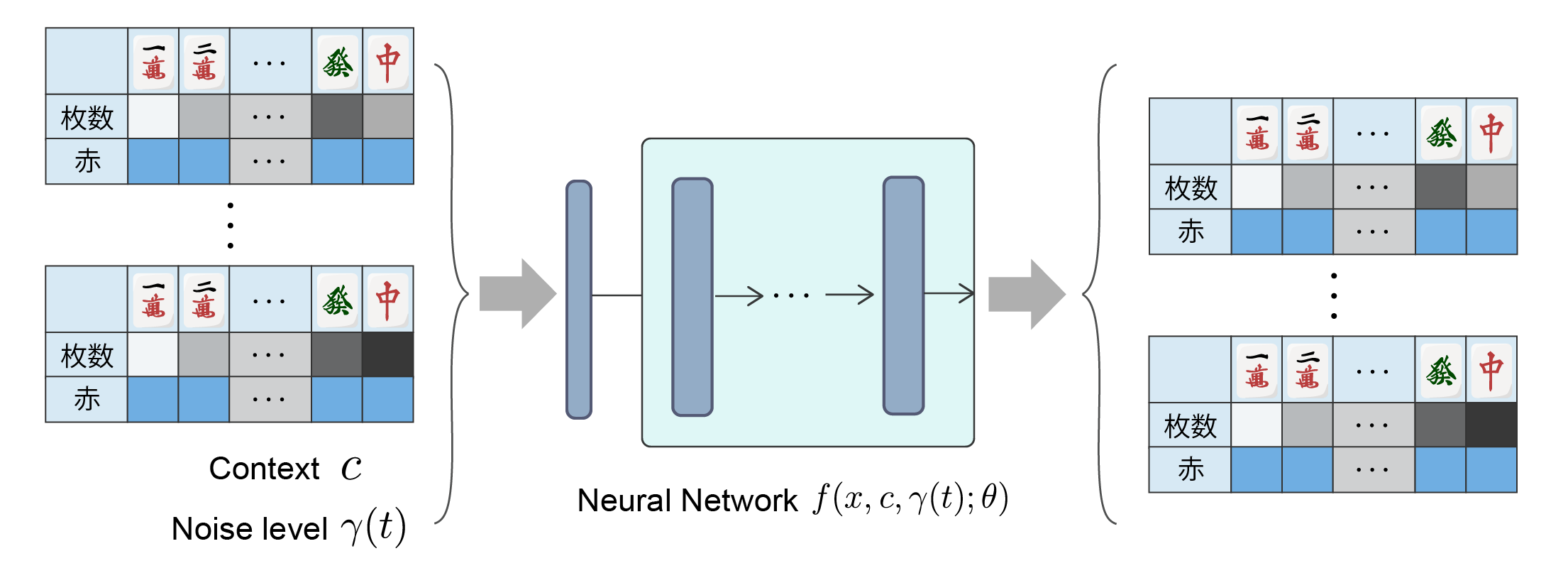
The neural network \(f\) has parameters \(\theta\), and predicts the clean hand vector \(x_{t=0}\) from the hand vector \(x_t\) at the time \(t\) of the diffusion process, the game state input \(c\) representing the discard and score situation observed from the generating player’s viewpoint, and the noise level \(\gamma(t)\) (Figure 2). The diffusion process uses Denoising Diffusion Probabilistic Models (DDPM, [Ho et al. 2020]), with a noise schedule using Cosine schedule. Additionally, Classifier-free guidance [Ho et al. 2022] was used to better reflect the conditional input. During generation, known self-hand tiles were replaced each time with denoising, similar to Inpainting in image generation, from the predicted clean hand \(x_{t=0}\) obtained from the trained model.

The number of tiles for each type is determined as follows to ensure the sum of the generated tile counts matches the limits of the opponent’s hand and the total number of tiles in the game:

1. Calculate the L1 distance between the count representation vector and the reference points \(\{0, 0.25, 0.5, 0.75, 1\}\) to get the count score.
2. Sort all count scores of the three generated players, and determine the number of tiles in order from the smallest count score.
3. Determine the number of tiles as \(\min(\text{[Total number of uncertain tiles in the hand]}, \text{[Number of uncertain tiles of that type in the game state]}, \text{[Count estimated from the count score]})\).
4. Once the number of tiles for each player is determined, it is not changed.
5. After evaluating all scores or reaching the target number of tiles, determine the presence of red dora by whether the score is above 0.5.

In the above procedure, there may be cases where the total number of tiles is insufficient even after evaluating all count scores, such as when the model output is all zeros. In such cases, tiles are randomly selected to fill in. However, in the experiments described later, the model sufficiently

trained did not require random tile filling.

Comparison Experiments with Autoregressive Model Using Tenhou Game Data

To evaluate the effectiveness of the proposed method, experiments were conducted using publicly available data from the online Mahjong site Tenhou [C-EGG], specifically 760,000 game logs from the Phoenix Table between 2012 and 2022. Of the dataset, 750,000 game logs were used as the training dataset, and the remaining 10,000 game logs were used as the evaluation dataset.

Existing research [Ogami et al.] evaluated using the number of matching tiles, but in Mahjong, there can be multiple hand candidates aiming for different yaku. Therefore, in this experiment, the distribution of Shanten numbers was compared as an indicator that can evaluate more varied generation results. The Shanten number is the number of tiles needed to replace to make the hand ready. The Shanten number of the generated hand is calculated, and the degree of change in its distribution with the progression of the game is compared to the dataset.

The structure of the proposed model was based on GPT [Radford et al.]. Additionally, an autoregressive model and a model that directly predicts Shanten numbers and waiting tiles without going through hand generation were trained for comparison. The autoregressive model had the same GPT-based structure as the proposed model, and the sequence of the training data consisted of tokens representing the hands of all four players. However, to express player differences, indices of the target player were added before and after the hands. The order of tiles in the sequence was not sorted as a hand but shuffled during training, considering that hands are set data. Preliminary experiments showed better performance with shuffled hands during training. For autoregressive model generation, necessary tiles were sampled according to the probability distribution of tile tokens rather than Beam Search. The direct prediction model was a baseline that estimated the Shanten number from the game state using a neural network without the constraint of generating a hand. It had the same model structure as the above two models and was trained with Cross-Entropy Loss. After training, each model generated 100 hands per game state for evaluation using the unseen dataset.

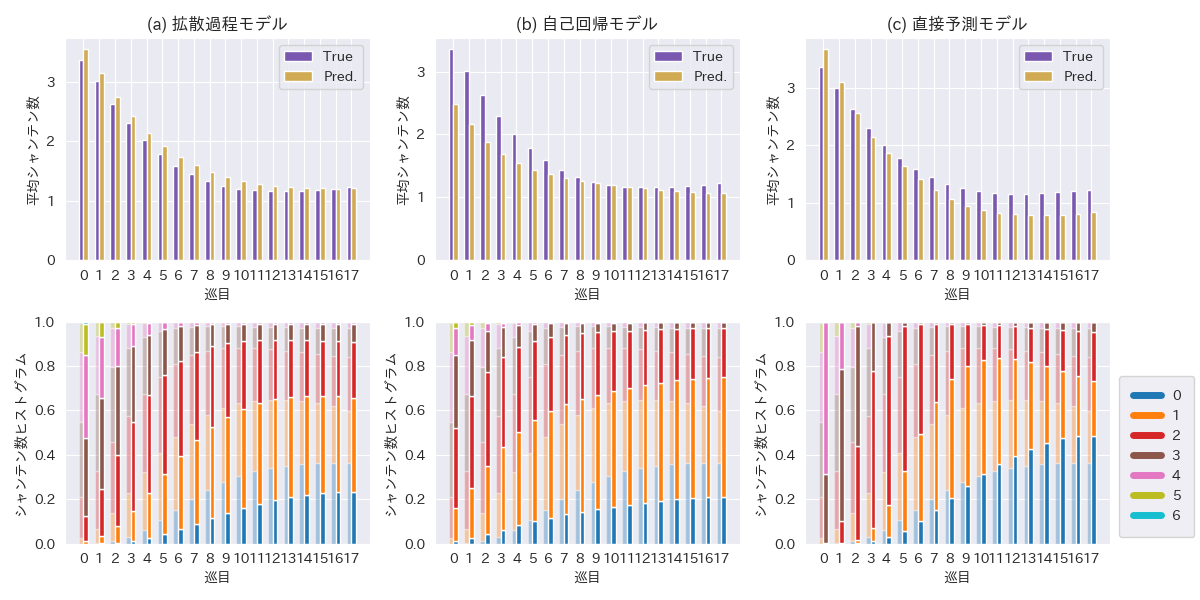
Table 1 shows the L2 error of the Shanten numbers for each method, and Figure 3 shows the transition of Shanten number distributions per turn. The L2 error was lower for the proposed method compared to the autoregressive method, and the direct prediction model had the smallest error. The Shanten number distribution trend for all methods was generally close to the dataset, but both the proposed and autoregressive methods had fewer zero Shanten (ready hands) frequencies. In contrast, the direct prediction model tended to have a higher proportion of one Shanten numbers compared to the dataset from turn 7 onwards.

Discussion

The experimental results showed that the proposed diffusion process model could generate hands with Shanten number distributions closer to the dataset compared to the autoregressive model. However, the proposed method tends to generate fewer ready hands. This is believed to be because the model struggles to create yaku structures with limited tile combinations, similar to generating hands or object structures in image generation models. Attempts to improve this situation, such as changing the coefficient of Classifier-free guidance or using Classifier guidance with a direct Shanten number prediction model, did not yield improvements. Other possible solutions include adding heuristics considering yaku when determining the number of tiles from the count representation. Regarding the computational cost of generation, it was possible to generate with less forward computation of the neural network compared to autoregression, but to apply it to large-scale simulations, further cost reduction is needed, such as reducing the number of steps in the diffusion process during generation using distillation.

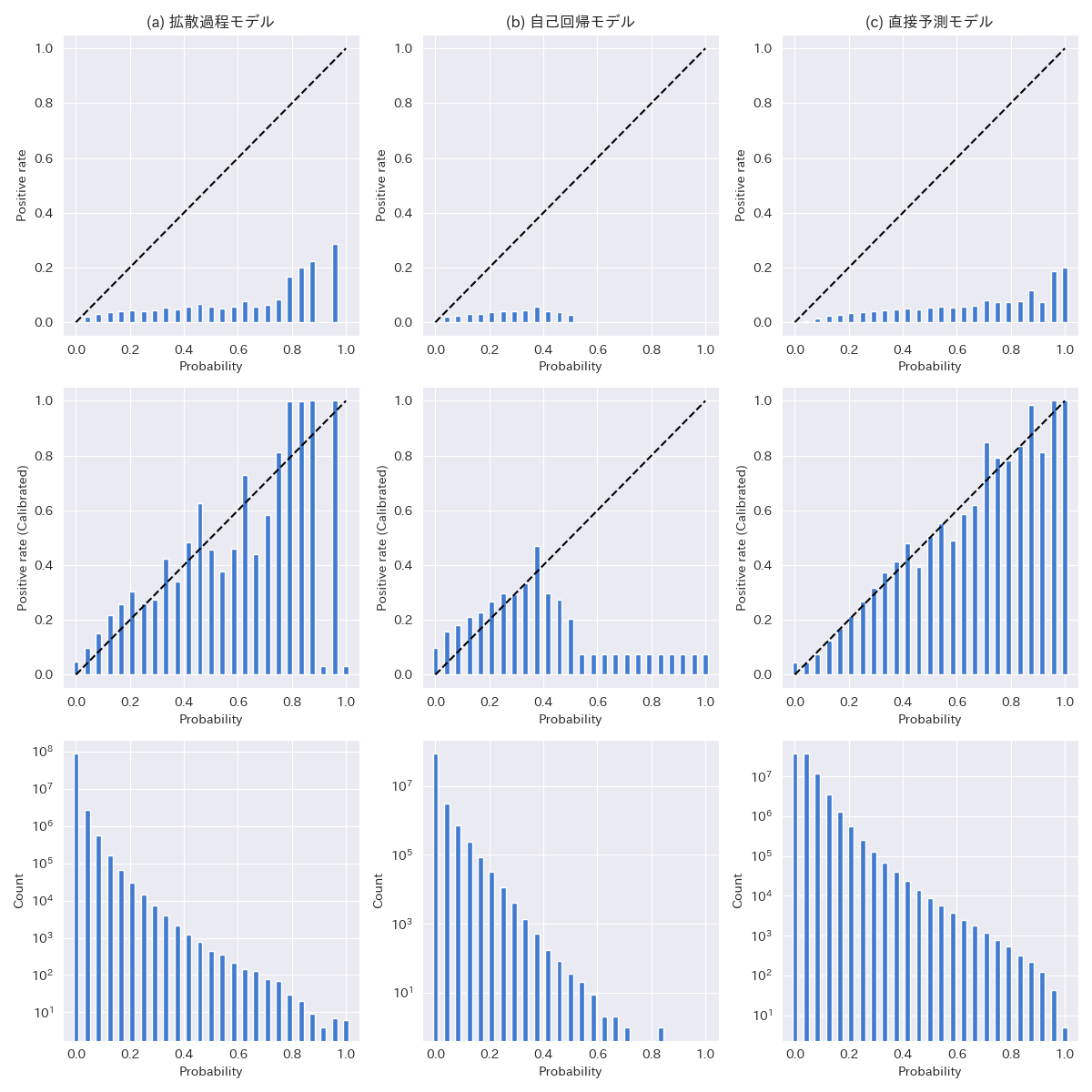
Another evaluation metric for hand estimation other than the Shanten number is the agreement of waiting tiles. Waiting tiles are the last tiles needed to complete a winning hand when in a ready state and are important information for deciding discard policies. Therefore, for the hand candidates generated in the experiment in the previous chapter, the proportion of each of the 34 types of tiles being waiting tiles was considered as the waiting tile probability, and this probability’s Calibration curve was compared (Figure 4). The Calibration curve is obtained by dividing the waiting tile probabilities into intervals and calculating the actual proportion of waiting tiles in each probability interval. The closer this curve is to y=x, the more the frequency of waiting tiles in the generated hands matches that in the dataset. However, since the frequency of waiting tiles in the game is low and the occurrence probability is not normalized, Platt Scaling [Platt. 1999] was used for calibration. Additionally, the prediction results of the direct prediction model using neural networks are also shown as a reference. Looking at the shape of the Calibration curve, the diffusion process model is closer to the y=x shape before and after calibration than the autoregressive method. The calibration loss weighted by the number of samples in each bin (Expected Calibration Error, ECE) was 0.00188 for the diffusion process and 0.00390 for autoregression. Additionally, similar to the Shanten number, the direct prediction model that predicted waiting tile scores directly without generating hands had the lowest calibration loss (ECE = 0.000801). However, due to the small number of samples collected in this experiment, the metrics from 0.5 to 1.0 probabilities may vary significantly depending on the choice of dataset.

As an application example using the proposed method, a demo was created to display the estimated opponent’s hands from any given situation. The slideshow below visualizes a portion of the estimated hands of the opponent from the perspective of the player at the bottom of the image. “Only Tenpai” filters the generated candidates to only those in the ready state. Additionally, the Shanten number is displayed next to the score in the situation display, indicating, for example, “S=1” means one away from Tenpai. Looking at the generated results in several situations, unnatural examples such as many four-of-a-kind in the autoregressive model were often seen, while the diffusion process model generated more natural-looking hands. It is known that autoregressive models tend to generate repeated words in natural language generation [Fu et al. 2021b], [Xu et al. 2022], and in this experiment, the same tile repetition pattern may be generated more easily for similar reasons.

The 2m tile was discarded early in the second turn by the player to the left, making it less likely for 1m, an outer tile of 2m, to be a waiting tile, and both models generated candidates avoiding 1m as a waiting tile. The second candidate of the diffusion process model appears unnatural as it is a 7s discard reach with an 8s single wait. The seventh hand of autoregression with a 9p single wait (one tile left in appearance) would be more natural if it had cut 4578s instead of 9p, as it would then be a non-standard four-way wait (11 tiles left in appearance), making a 9p single wait unnatural.

The opponent to the right called Chi with 7s for 789. Both 發 and 中 are two tiles cut, and 北 (self-wind) is three tiles cut in this situation. The diffusion process model reflects well that it is likely a white dragon back or a straight hand. The autoregressive model generated many cases that would result in no yaku.

The opponent to the right discarded tiles from the middle of each suit, indicating a high possibility of mixed or pure straight. Both diffusion and autoregressive models seem to understand that mixed or pure straight is highly likely. However, there are cases where the models do not properly understand the information of the last 9p discard (if generating such hands, discarding 9p in the previous turn would be unnatural). This tendency is stronger in the autoregressive model.

The opponent to the left seems to be going for a flush based on their discards. The diffusion process model almost certainly concludes a flush in bamboos, while the autoregressive model considers other possibilities. The autoregressive model often generates unnatural hands with many non-kan tiles. The second hand of the autoregressive model is unnatural because if it had cut 4s instead of 東, it would be guaranteed a flush and possibly a mixed straight.

Conclusion

This article introduced a method for constructing an opponent’s hand generation model using the diffusion process for estimating imperfect information in Mahjong AI simulation. To handle hidden hands as variable-length set data (discrete data) with existing continuous data diffusion process models, we converted them to a count representation and proposed a discretization method using the predicted counts during generation. The results of training with human game data showed that the proposed method could generate hands with Shanten number distributions closer to the dataset compared to existing autoregressive models. Future developments could include improvements for generating ready hands, which both the proposed and autoregressive models struggle with, and applications to simulation.

Author

Publish: 2023/12/12

Kazuma Sasaki