本記事の内容は麻雀AI「NAGA」の牌譜サービスで利用されているアルゴリズムとは直接関連のない基礎的な研究の内容になります。
不完全情報ゲームである麻雀でシミュレーションや方策のサンプリングを精緻に行うためには不確定な情報の推定が必要である．特に相手プレイヤーの手牌は戦略に大きく影響する情報だが，一般にその分布を数え上げで求めることは困難である．そのため実際の牌譜データを用いた機械学習による手牌の推定方法として自己回帰ニューラルネットを用いた最尤推定などが提案されてきた．しかしシミュレーションを行うためには最も尤もらしい手牌予測のみを得るのではなく，実際のデータセットの分布に沿った手牌サンプルを高速に生成できる必要がある．そこで画像データなどで近年注目されている拡散過程モデルを用いることで，実際の分布に近いサンプルをより低計算コストで生成する手法を提案する．一般的な拡散過程モデルは画像や音声のような連続データを扱うのに対して，麻雀の手牌は離散なセットデータであるため，手牌を各牌種の枚数表現を連続ベクトルとしてみなすことで既存の拡散過程モデルの学習法を適用可能にした．インターネット麻雀サイト天鳳の牌譜を用いた実験を行ったところ， Transformer を用いた自己回帰モデルと比べてよりシャンテン数の分布が実際のデータと近いことがわかった．また生成された手牌とデータセット中の手牌の待ち牌の出現率の傾向の比較と具体的な局面における生成例を紹介する．
麻雀は世界中で遊ばれているポピュラーなゲームの1つであり，様々な自動プレイができるAIエージェントの研究が行われている．近年の代表的なアプローチは大規模な人間の牌譜データと自己対戦を用いた深層強化学習だが [Li et al. 2020, Fu et al. 2021a, Li et al. 2022, Zao et al. 2022] ，麻雀のような多人数ゲームではシミュレーションを用いた探索によってより効率的な学習が行える可能性がある．たとえば Counterfactual Regret Minimization [Zinkevich et al.] やモンテカルロ探索木探索による価値推定 [Mizukami et al.] などはゲーム木を展開することにより，ゲームの確率論的な性質をより考慮した精緻な価値や方策の近似が行える．ただし，麻雀は山や相手の手牌など現在の状態に不確定な情報が含まれている不確定情報ゲームである．シミュレーションは現在の局面の状態から未来の状態を計算する必要があるため，不確定情報ゲームである麻雀には直接適用できない．また麻雀は局面がとりうるバリエーションが非常に多いため総当たりのシミュレーションは困難である．こうした不確定情報の扱いの難しさから，深層強化学習による麻雀AIでは方策の潜在空間の制約として利用する [Han et al.] など，不確定情報の具体的なサンプリングは避けられている．
麻雀の不確定情報のうちでゲーム結果に大きく影響する要素の1つは相手プレイヤーの手牌である．手牌は自分の手牌，捨てられた牌（河），鳴きなどですでに分かっている牌を除いた未確定な牌による組み合わせで確率的に表すことができる．しかし，これでもありうる手牌のバリエーションは多く，具体的な分布を数え上げで求めることは困難である．そのため既存の手牌推定では CRF [Nemoto et al.] などを用いた機械学習による方法が提案されてきた．特に近年では Transformer がその性能の高さから注目されており，手牌を表す牌トークンのシーケンスを局面状態を条件入力とした自己回帰によって学習している．[Ogami et al.] は Transformer モデルの予測を用いた Beam Search による生成でランダム推定と比べて牌の種類が実際のデータと合致する手牌候補を推定できることを報告している．しかしながら，精度の良いシミュレーションを行うためには最も尤もらしい手牌予測のみを得るのではなく，実際のデータセットの分布に沿った手牌サンプルを複数生成できる必要がある．また自己回帰による生成では相手の手牌の長さ分だけ前向き計算が必要であり，計算コストが高いという問題もある．
そこで我々は拡散過程を用いた手牌生成手法を提案する．手牌推定は局面状態を条件としたデータ生成問題であるとみなせるが，近年では画像や動画などで拡散過程モデルがよく使われている．拡散過程モデルはデータへ逐次的にノイズが付加され拡散していく過程の逆過程をニューラルネットで近似する手法であり，安定した学習と多様かつ品質の良いサンプルを生成できることが知られている [Song et al.] また生成時の拡散過程の系列長は生成データの長さとは独立して決めることができるため，自己回帰モデルに比べて少ない計算コストで生成できる可能性がある．しかし既存の拡散過程モデルが主に生成対象としているのは画素値のような実数値のベクトルであるのに対して，麻雀の手牌は離散なセットデータである．離散値を連続値へ変換して拡散過程を使う方法として Bit Diffusion [Checn et al.] などがあるが，麻雀の手牌のような可変長なセットデータへの応用は行われていない．そこで我々は各牌種の枚数を用いて手牌を実数値ベクトルとして表現し，既存の拡散過程モデルによる学習を可能した．生成時には学習済みモデルによって得られた枚数表現ベクトルから具体的な手牌へと変換するために，ありうる牌の枚数上限を超えないようサンプリングを行う．
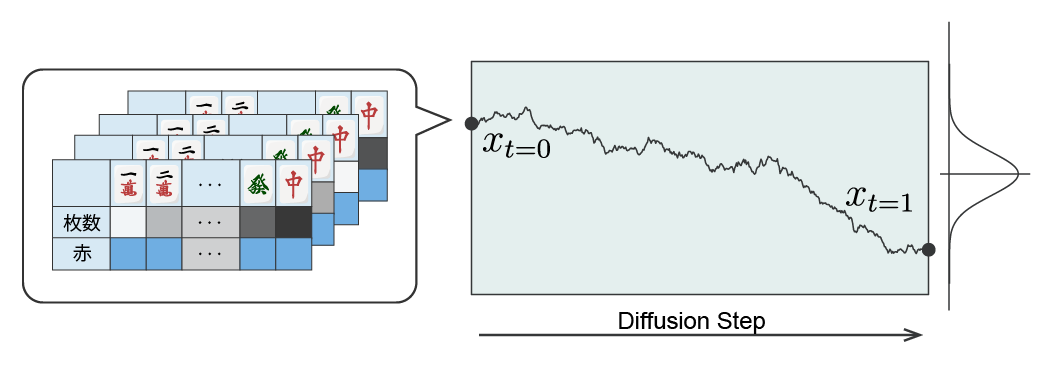
今回は日本でポピュラーな四麻のリーチ麻雀を扱う．卓にある牌は34種類の牌と4枚ずつであり，赤ドラがあるものとする．提案手法は4人のプレイヤーのうち，ある1人のプレイヤーの視点が得られる山やドラ，点数状況，自分の手牌など確定情報から相手の手牌を生成する．手牌は鳴きに応じて枚数が異なる可変長データであり，かつ牌の順番を変えても変わらないセットデータである．対して一般的な拡散過程モデルが扱えるのは固定長の連続ベクトルである．そこで34の牌種の枚数と赤ドラの有無を固定長の連続ベクトルで手牌を表現し，このベクトルの拡散過程
を考える（図1）．具体的には取りうる牌の枚数 \( \{0, 1, 2, 3 \}\) を \( [0, 1] \) の範囲に収まるように線形補間した枚数の基準点 \( \{0 , 0.25, 0.5 , 0.75, 1\}\) で変換した34次元のベクトルと，赤牌の有無を示す \( \{0, 1\} \) の34次元ベクトルを合わせた 2 x 34 次元のベクトルを1人分の手牌とし，これを推論時の主観視点のプレイヤー自身も含めた4人分を集めた 4 x 2 x 34 次元の連続値ベクトル \( x \) を生成対象とする．そして，このベクトルが標準正規分布へ拡散する過程を考え，この逆過程をニューラルネットワーク \( f \) で学習する．
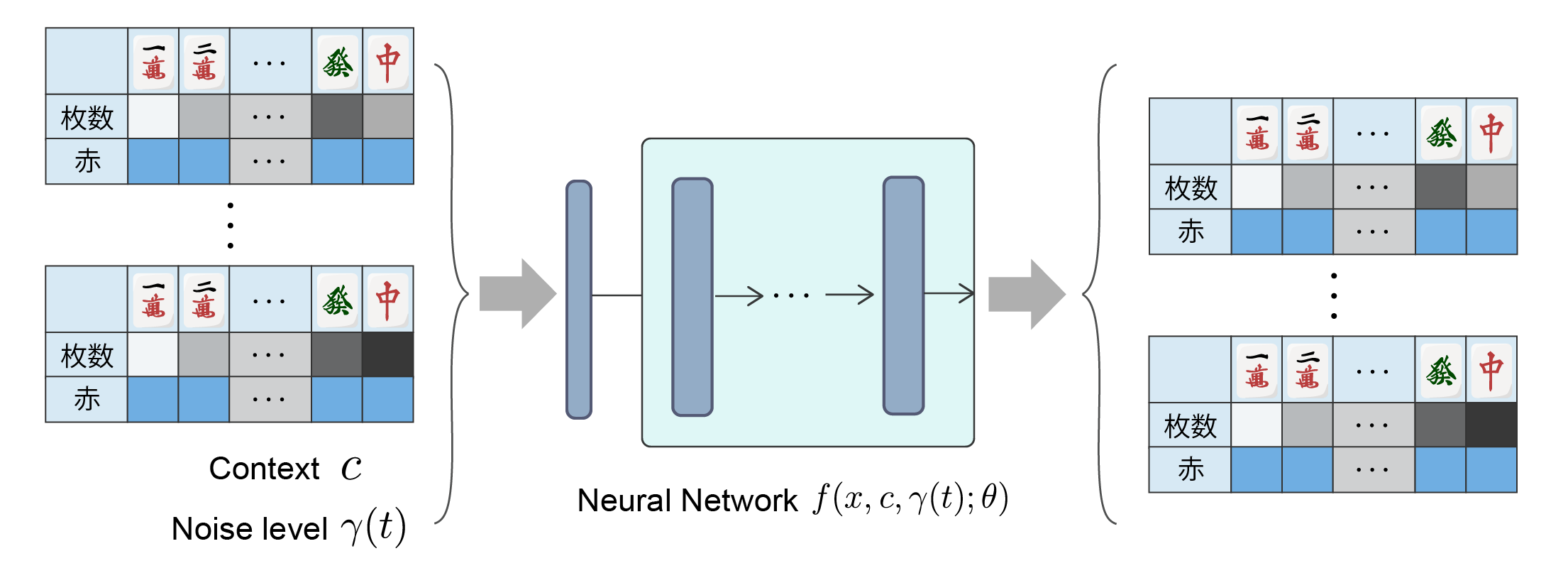
ニューラルネットワーク \( f \) はパラメータ \( \theta \) をもち，拡散過程の時刻 \( t \) における前述の手牌ベクトル \( x*t \) と生成時のプレイヤー視点から観測できる捨て牌や得点状況などをあらわす局面状態入力 \( c \) ，ノイズレベル \( \gamma(t) \) を受けクリーンな手牌ベクトル \( x*{t=0} \) を予測するように学習される（図2）．拡散過程は Denoising Diffusion Probabilistic Models (DDPM, [Ho et al. 2020])を用い，ノイズスケジュールは Cosine schedule を用いた．また条件入力をより反映させるため Classifier-free guidance [Ho et al. 2022] を用いた．学習後の生成では一定ステップ数の拡散過程を経て生成された \( x\_{t=0} \) から具体的な手牌へと変換するが，この過程の途中で画像生成における Inpainting と同様に既知である自らの手牌を都度置き換えてデノイジングを行った．
生成時には相手の手牌枚数とゲーム全体での牌の枚数の上限が決まっているが，生成された牌の枚数表現の総和は必ずしも一致しない．そこで以下のようなルールで各牌種の枚数を決定する:
上記の手順では，たとえばモデルの出力が全種類0枚になった場合など，すべての枚数スコアを評価したあとでも手牌の枚数が足りない場合がある．この場合はランダムに牌を選択し埋める．ただし後述する実験においては，学習が十分に進んだモデルではランダム牌による埋めは発生しなかった．
提案手法の有効性を評価するため，オンライン麻雀サイト天鳳 [C-EGG] の公開データの内，2012年から2022年の牌譜の一部である鳳凰卓の76万半荘分を用いた実験を行った．データセットのうち75万半荘分を学習データセットとし，残りの1万半荘分を評価用データセットとした．
既存研究 [Ogami et al.] では牌の一致枚数を用いて評価していたが，麻雀では異なる役を目指す複数の手牌候補がありうる．そこで今回の実験ではよりバリエーションのある生成結果を評価できる指標として，シャンテン数の分布を比較する．シャンテン数とは，手牌をテンパイしている状態にするために入れ替えが必要な牌の枚数のことである．生成された手牌のシャンテン数を計算し，その分布が巡目（ゲームの進行）に応じて変化する度合いをデータセットと比較する．
提案モデルの構造は GPT [Radford et al.] をベースにした．また，比較対象として自己回帰モデル，そして手牌生成を経由せずシャンテン数と待ち牌を直接予測するモデルを学習した．自己回帰モデルは提案モデルと同様にGPTベースのモデル構造とし，学習データのシーケンスは全プレイヤー4人分の手牌を示すトークンを並べたものとした．ただしプレイヤーの違いを表現するため手牌の前後には対象プレイヤーのインデックスを加えた．シーケンスにおける牌の順番は手牌がセットデータであることを考慮し，学習時には手牌の並びは理牌(ソート)された形ではなく、シャッフルした状態で学習した．なお，予備実験において比較したところ学習時のシャッフル有りの場合の方が性能がよかった．自己回帰モデルの生成には Beam Search ではなく牌トークンの確率分布にしたがって必要な枚数分サンプリングする方式を採った．直接予測モデルは手牌を生成するという制約なしに局面状態からシャンテン数をニューラルネットワークで推定するベースラインである．上記2つのモデルと同様のモデル構造であり，Cross-Entropy Loss で損失を計算し学習をおこなった．学習後にそれぞれのモデルについて未学習データセットで1局面あたり100個の手牌を生成し評価した．
| 拡散モデル | 自己回帰モデル | 直接予測モデル | |
|---|---|---|---|
| L2誤差 | 1.00 ± 0.75 | 1.03 ± 0.78 | 0.86 ± 0.64 |
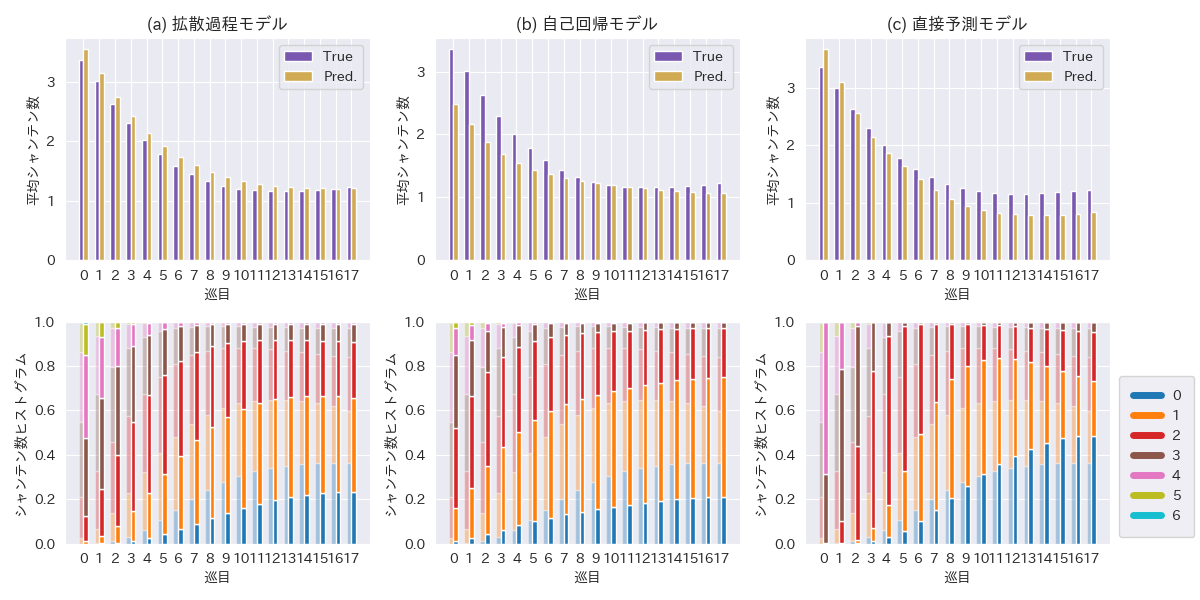
表1に各手法のシャンテン数のL2誤差を，図3に巡目ごとのシャンテン数の分布の推移を示す．手牌を推定する手法では自己回帰に比べ提案手法のL2誤差が少なく，すべての手法においては直接予測モデルの誤差が小さかった．シャンテン数の分布についてはいずれの手法でもデータセットの分布とおおむね近い傾向がみられるものの，提案手法・自己回帰ともにシャンテン数0，つまり聴牌の頻度が少なかった．対して直接予測モデルは7巡目以降からシャンテン数1の割合がデータセットに比べて多くなる傾向があった．
実験結果より，提案手法の拡散過程モデルが自己回帰よりもデータセットに近いシャンテン数の分布をもつ手牌を生成できることがわかった．しかしながら，提案手法は聴牌した手牌が生成されづらい傾向がある．これは画像生成モデルにおける人物の手や物体の構造と同様に，限られた牌の組み合わせで役の構造を作ることをモデルが苦手としているからであると考えられる．Classifier-free guidance の係数を変更したり，シャンテン数の直接予測モデルを使った Classifier guidance なども試したが状況は改善しなかった．他の対策方法として牌の枚数表現からの枚数を決定する際に役を考慮したヒューリスティックを加える方法などが考えられる．また生成の計算コストに関しては自己回帰よりも少ないニューラルネットワークの前向き計算で生成が行えたものの，大規模なシミュレーションに応用するためには蒸留などを用いて生成時の拡散過程のステップ数を減らすなど，よりコストを削減する必要があるだろう．
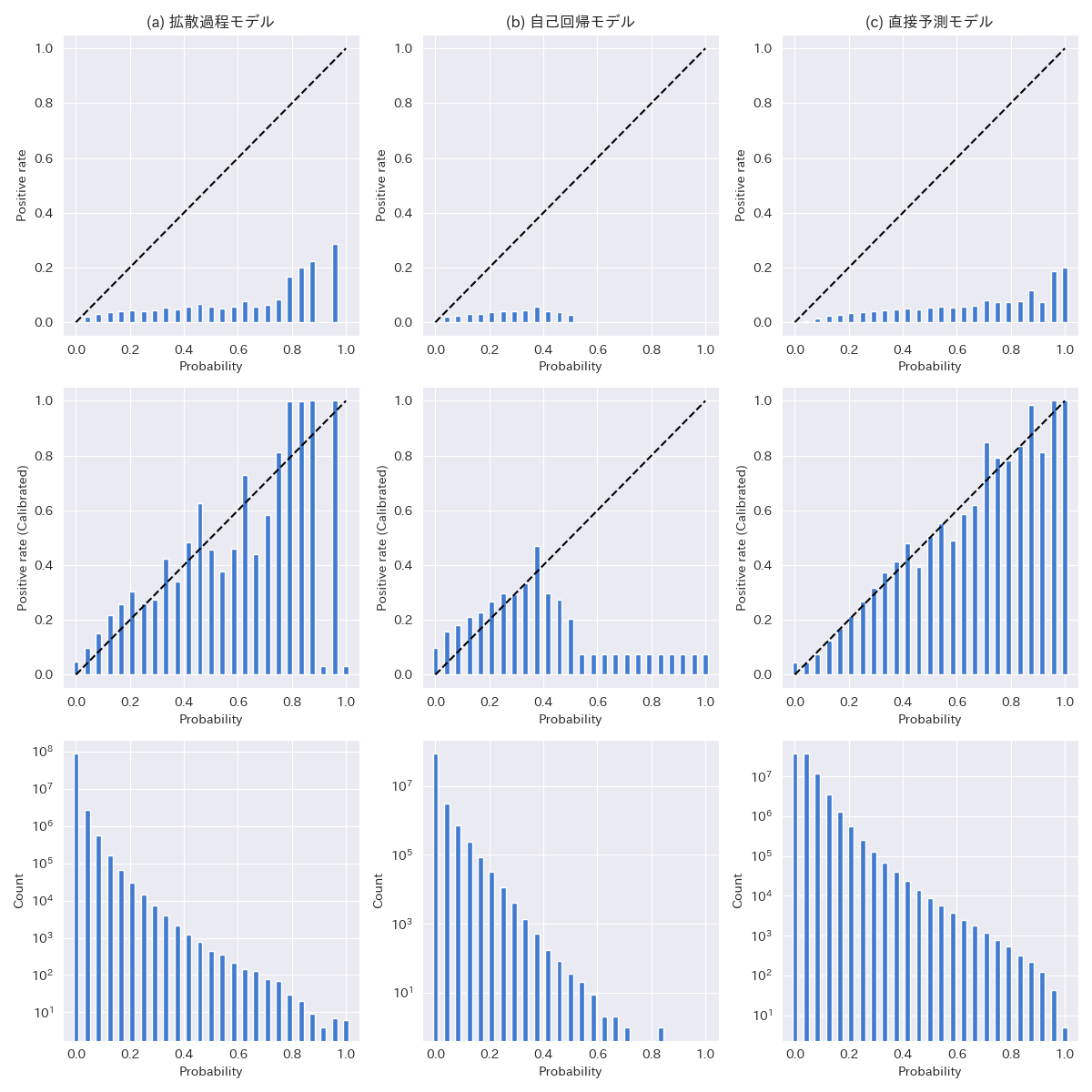
シャンテン数以外の手牌推定の評価指標として待ち牌の一致度がある．待ち牌は聴牌の場合にアガリに必要な最後の牌であり，捨て牌を決定する方策にとって重要な情報である．そこで，前章での実験において生成された手牌候補について各34種類の牌が待ち牌になっている割合を待ち牌確率とみなし，この確率の Calibration curve を比較した（図4）．Calibration curve は待ち牌確率を一定の間隔で分割し，各々の確率の局面において実際に待ち牌だった割合を求めることで得られる．この曲線が y=x に近いほど，生成される手牌とデータセット中の待ち牌の頻度が一致していることを示す．ただし待ち牌が存在するゲーム中における頻度が少なく，出現確率が正規化されていないため Platt Scaling [Plat. 1999] を用いてキャリブレーションを行った．また，こちらも参考値としてニューラルネットを使った直接予測モデルの予測結果も併記した．Calibration curve の形をみると拡散過程モデルが自己回帰の場合よりもキャリブレーション前後でどちらでも y=x の形状に近いことがわかる．各サンプル数で重み付けしたキャリブレーション損失 (Expected Calibration Error, ECE) を求めたところ，拡散過程は 0.00188，自己回帰は 0.00390 だった．またシャンテン数と同様に拡散過程・自己回帰よりも手牌生成を経ずに直接待ち牌スコアを予測する直接予測の方がキャリブレーション損失が低かった（ECE = 0.000801）．ただし，今回の実験において収集できたサンプル数が少ないことから，確率0.5前後から1.0の間の指標はデータセットの選び方如何で結果が大きく変わる可能性がある．
提案手法を用いたアプリケーション例として，任意の局面から推定される相手プレイヤーの手牌を表示するデモを作成した．以下のスライドショーは画像中下側のプレイヤーから見た相手プレイヤーの手牌の推定結果の一部を可視化したものである．「聴牌のみ」は生成された候補のうち，聴牌形になっているものだけを絞り込んだ結果である．また局面表示の点数の横にシャンテン数を表示してあり，たとえば「S=1」は1向聴であることを示す．いくつかの局面における生成結果をみたところ，自己回帰の生成結果には同種四枚形が多いなど不自然な例が散見されるのに対して拡散過程モデルの方は自然にみえる手牌を出す例が多かった．自己回帰モデルは自然言語生成の際に同じ語の繰り返しを生成しやすいことが知られており [Fu et al. 2021b], [Xu et al. 2022],今回の実験においても同様の理由で同じ牌の繰り返しパターンが生成されやすい可能性がある．
上家の2巡目の 2m が早く切られており，その外側の牌である 1m が待ちになりにくいと考えられるが，どちらのモデルも 1m が待ちになるケースを避けた候補を生成している． 拡散過程の2つめの候補は 7s 切りリーチで 8s の単騎待ちになるのは不自然にみえる． 自己回帰の7つ目の 9p 単騎(見た目1枚残り)の手牌は，7s 切りではなく 9p を切っていれば 4578s の変則4門張(見た目11枚残り)となるため，9p 単騎となるのは不自然．
対面が 7s を 789 でチーしている．發中東は2枚切れ，北(自風)は3枚切れの局面． 拡散過程モデルは役牌の白バックか一気通貫のどちらかの可能性が高いということをよく反映している． 三色同順も枚数的には有り得るが、切り順等からあまり無さそうと判断していると思われる． 自己回帰モデルは役無しになりそうなケースも多く生成している．
対面は切り出しが各色の真ん中から切られており、混全帯么九や純全帯幺の可能性が高そう． 拡散過程・自己回帰共に混全帯么九や純全帯幺の可能性が高そうということは理解していそうである． ただし最後の 9p 手出しに関しての情報をきちんと理解していないと思われるケース(仮に生成した手牌だとすると前順で 9p を切ることが不自然であるケース)がある．特に自己回帰はその傾向が強い．
上家の捨て牌から染め手と思われる． 拡散過程は索子の混一色だとほぼ断定しているが，自己回帰はそれ以外の可能性もあると見ている． 自己回帰は暗槓せずに4枚の同種字牌が多く含まれるケースが多く不自然なものが多い．自己回帰の2つ目の手牌は，東を切らずに 4 sを切っていれば混一色確定かつ混全帯么九の可能性もあるため不自然．
この記事では麻雀AIにおけるシミュレーションを前提とした不完全情報の推定として相手プレイヤーの手牌生成モデルを拡散過程を用いて構築する方法を紹介した．可変長なセットデータ（離散データ）である隠れた手牌を既存の連続データの拡散過程モデルで扱うために枚数表現への変換を行い，生成時には生成された枚数の予測値を使った離散化の手法を提案した．人間の牌譜データを用いた学習の結果，提案手法は既存の自己回帰モデルに比べてシャンテン数の分布が近い手牌を生成できることがわかった．今後の発展として提案手法と自己回帰モデルが苦手としている聴牌形の生成のための工夫や，シミュレーションへの応用などが考えられる．
[li2020] Li, Junjie, Sotetsu Koyamada, Qiwei Ye, Guoqing Liu, Chao Wang, Ruihan Yang, Li Zhao, Tao Qin, Tie-Yan Liu, and Hsiao-Wuen Hon. 2020. “Suphx: Mastering Mahjong with Deep Reinforcement Learning.” arXiv preprint arXiv:2003.13590 https://arxiv.org/abs/2003.13590
[fu_a] Fu, Haobo, Weiming Liu, Shuang Wu, Yijia Wang, Tao Yang, Kai Li, Junliang Xing, et al. 2021. “Actor-Critic Policy Optimization in a Large-Scale Imperfect-Information Game.” International Conference on Learning Representations. https://openreview.net/forum?id=DTXZqTNV5nW
[li2022] Li, Jinqiu, Shuang Wu, Haobo Fu, Qiang Fu, Enmin Zhao, and Junliang Xing. 2022. “Speedup Training Artificial Intelligence for Mahjong via Reward Variance Reduction.” IEEE Conference on Games (CoG), 345–52. https://ieeexplore.ieee.org/document/9893584
[zao] Zhao, Xiangyu, and Sean B. Holden. 2022. “Building a 3-Player Mahjong AI Using Deep Reinforcement Learning.” arXiv preprint arXiv:2202.12847. https://arxiv.org/abs/2202.12847
[zinkevich] Martin Zinkevich, Michael Johanson, Michael Bowling, and Carmelo Piccione. 2007. Regret minimization in games with incomplete information. In Proceedings of the 20th International Conference on Neural Information Processing Systems. 1729–1736. https://papers.nips.cc/paper_files/paper/2007/hash/08d98638c6fcd194a4b1e6992063e944-Abstract.html
[mizukami] Mizukami, Naoki, and Yoshimasa Tsuruoka. 2015. “Building a Computer Mahjong Player Based on Monte Carlo Simulation and Opponent Models.” IEEE Conference on Computational Intelligence and Games (CIG), 275–83. https://ieeexplore.ieee.org/document/7317929
[han] Han, D., Kozuno, T., Luo, X., Chen, Z. Y., Doya, K., Yang, Y., & Li, D. 2021. Variational oracle guiding for reinforcement learning. In International Conference on Learning Representations. https://openreview.net/pdf?id=pjqqxepwoMy
[nemoto] 根本佳典, 古宮嘉那子, 小谷善行. 2012. "CRF を用いた麻雀の不完全情報推定." ゲームプログラミングワークショップ 2012 論文集 2012.6. 155-158. https://ipsj.ixsq.nii.ac.jp/ej/?action=pages_view_main&active_action=repository_view_main_item_detail&item_id=91363&item_no=1&page_id=13&block_id=8
[ogami] 大神 卓也, 奈良 亮耶, 天野 克敏, 今宿 祐希, 鶴岡 慶雅. 2022. “Transformerを用いた麻雀における手牌推定.” ゲームプログラミングワークショップ2022論文集, 151–58. https://ipsj.ixsq.nii.ac.jp/ej/?action=pages_view_main&active_action=repository_view_main_item_detail&item_id=222007&item_no=1&page_id=13&block_id=8
[song] Song, Yang, Jascha Sohl-Dickstein, Diederik P. Kingma, Abhishek Kumar, Stefano Ermon, and Ben Poole. 2020. “Score-Based Generative Modeling through Stochastic Differential Equations.” International Conference on Learning Representations. https://arxiv.org/abs/2011.13456
[chen] Chen, Ting, Ruixiang Zhang, and Geoffrey Hinton. 2023. “Analog Bits: Generating Discrete Data Using Diffusion Models with Self-Conditioning.”, In International Conference on Learning Representations. https://openreview.net/forum?id=3itjR9QxFw
[ho2020] Ho, Jonathan, Ajay Jain, and Pieter Abbeel. 2020. "Denoising diffusion probabilistic models." Advances in neural information processing systems 33: 6840-685. https://arxiv.org/abs/2006.11239
[ho2022] Ho, Jonathan, and Tim Salimans. 2022. "Classifier-free diffusion guidance." arXiv preprint arXiv:2207.12598. https://arxiv.org/abs/2207.12598
[c-egg] C-EGG, オンライン対戦麻雀 天鳳(てんほう), Accessed October 4, 2023. https://tenhou.net/
[radford] Radford, Alec, Karthik Narasimhan, Tim Salimans, and Ilya Sutskever. n.d. “Improving Language Understanding by Generative Pre-Training.” Accessed October 4, 2023. https://cdn.openai.com/research-covers/language-unsupervised/language_understanding_paper.pdf
[platt] Platt, John. Probabilistic outputs for support vector machines and comparisons to regularized likelihood methods. Advances in large margin classifiers. 1999. Advances in large margin classifiers 10.3: 61-74.
[fu_b] Fu, Z., Lam, W., So, A. M. C., & Shi, B. 2021. A theoretical analysis of the repetition problem in text generation. In Proceedings of the AAAI Conference on Artificial Intelligence. Vol. 35, No. 14, pp. 12848-12856. https://arxiv.org/abs/2012.14660
[xu] Xu, J., Liu, X., Yan, J., Cai, D., Li, H., & Li, J. 2022. Learning to break the loop: Analyzing and mitigating repetitions for neural text generation. Advances in Neural Information Processing Systems, 35, 3082-3095. https://arxiv.org/abs/2206.02369
Kazuma Sasaki
